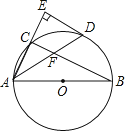
题目内容
【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时从点C出发,以1cm/s的速度分别沿CA、CB匀速运动.当点Q到达点B时,点P、Q同时停止运动.过点P作AC的垂线l交AB于点R,连接PQ、RQ,并作△PQR关于直线l对称的图形,得到△PQ′R.设点Q的运动时间为t(s),△PQ′R与△PAR重叠部分的面积为S(cm2).
(1)t为何值时,点Q′恰好落在AB上?
(2)求S与t的函数关系式,并写出t的取值范围;
(3)S能否为 ![]() cm2?若能,求出此时的t值;若不能,说明理由.
cm2?若能,求出此时的t值;若不能,说明理由.
【答案】
(1)
解:连接QQ′,
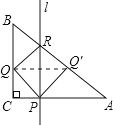
∵PC=QC,∠C=90°,
∴∠CPQ=45°,又l⊥AC,
∴∠RPQ=∠RPC﹣∠CPQ=90°﹣45°=45°,
由对称可得PQ′=PQ,∠QPQ′=90°,QQ′=2t,且QQ′∥CA,
∴∠BQQ′=∠BCA,又∠B=∠B,
∴△BQQ′∽△BCA,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t=2.4;
(2)
解:当0<t≤2.4时,过Q′作Q′D⊥l于D点,则Q′D=t,
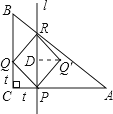
又∵RP∥BC,
∴△RPA∽△BCA,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴RP=(8﹣t) ![]() =
= ![]() ,
,
∴S= ![]() RPQ′D=
RPQ′D= ![]()
![]() t=﹣
t=﹣ ![]() t2+3t;
t2+3t;
当2.4<t≤6时,记PQ′与AB的交点为E,过E作ED⊥l于D,
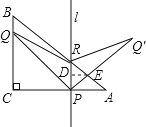
由对称可得:∠DPE=∠DEP=45°,
又∵∠PDE=90°,
∴△DEP为等腰直角三角形,
∴DP=DE,
∵△RDE∽△BCA,
∴ ![]() =
= ![]() =
= ![]() ,即DR=
,即DR= ![]() DE,
DE,
∵△RPA∽△BCA,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴RP= ![]() ,
,
∴RP=RD+DP=DR+DE=DE+ ![]() DE=
DE= ![]() ,即
,即 ![]() DE=
DE= ![]() ,
,
∴DE= ![]() ,
,
∴S= ![]() RPDE=
RPDE= ![]()
![]()
![]() =
= ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() ;
;
(3)
解:S能为 ![]() cm2,理由为:
cm2,理由为:
若 ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() =
= ![]() (2.4<t≤6),
(2.4<t≤6),
整理得:t2﹣16t+57=0,
解得:t= ![]() =8±
=8± ![]() ,
,
∴t1=8+ ![]() (舍去),t2=8﹣
(舍去),t2=8﹣ ![]() ;
;
若﹣ ![]() t2+3t=
t2+3t= ![]() (0<t≤2.4),
(0<t≤2.4),
整理得:t2﹣8t+3=0,
解得:t= ![]() =4±
=4± ![]() ,
,
∴t1=4+ ![]() (舍去),t2=4﹣
(舍去),t2=4﹣ ![]() ,
,
综上,当S为 ![]() cm2时,t的值为(8﹣
cm2时,t的值为(8﹣ ![]() )或(4﹣
)或(4﹣ ![]() )秒
)秒
【解析】(1)如图所示,连接QQ′,由题意得到三角形PQC为等腰直角三角形,可得出∠CPQ=45°,再由l与AC垂直,得到∠RPQ也为45°,进而由对称性得出PQ′=PQ,∠QPQ′=90°,QQ′=2t,且QQ′∥CA,由平行得到一对同位角相等,再由公共角相等,利用两对对应角相等的两三角形相似得到△BQQ′∽△BCA,由相似得比例,将各自的值代入列出关于t的方程,求出方程的解即可得到此时t的值;(2)由(1)求出t的值,分两种情况考虑:当0<t≤2.4时,过Q′作Q′D⊥l于D点,则Q′D=t,由RP与BC平行,利用两直线平行得到两对同位角相等,利用两对对应角相等的两三角形相似得到△RPA∽△BCA,由相似得比例表示出RP,利用三角形的面积公式表示出S关于t的关系式即可;当2.4<t≤6时,记PQ′与AB的交点为E,过E作ED⊥l于D,由对称性得到由对称可得:∠DPE=∠DEP=45°,可得出三角形DEP为等腰直角三角形,得到DE=DP,由△RDE∽△BCA,利用相似得比例,表示出DR,再由△RPA∽△BCA,由相似得比例,表示出RP,由RP=RD+DP=RD+DE,将表示出的DR及RP代入,表示出DE,利用三角形的面积公式即可表示出S与t的关系式;(3)S能为 ![]() cm2 , 具体求法为:当0<t≤2.4时,令S=
cm2 , 具体求法为:当0<t≤2.4时,令S= ![]() ,得出关于t的一元二次方程,求出方程的解得到t的值;当2.4<t≤6时,令S=
,得出关于t的一元二次方程,求出方程的解得到t的值;当2.4<t≤6时,令S= ![]() ,得出关于t的一元二次方程,求出方程的解得到t的值,经检验得到满足题意t的值.
,得出关于t的一元二次方程,求出方程的解得到t的值,经检验得到满足题意t的值.
【考点精析】掌握求根公式和勾股定理的概念是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 阅读快车系列答案
阅读快车系列答案【题目】某校初二年级数学考试,(满分为100分,该班学生成绩均不低于50分)作了统计分析,绘制成如图频数分布直方图和频数、频率分布表,请你根据图表提供的信息,解答下列问题:
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 | a | 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |

(1)频数、频率分布表中a= ,b= ;(答案直接填在题中横线上)
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.