题目内容
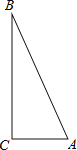
【题目】(1)如图1,∠A=60°,AC=1,AB=2求BC的长;
(2)如图2,在△ABC中,试证明:BC2=AC2+AB2-2AC![]() ABcosA.
ABcosA.
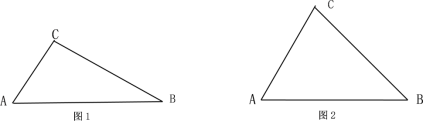
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
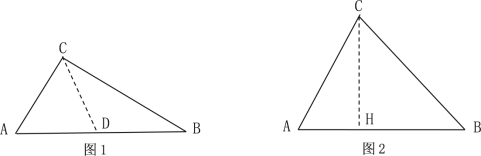
(1)取AB的中点D,连结CD ,易证△ACD为等边三角形,然后可得AC=AD=DC=BD=1,求出∠B=30°,∠ACB=90°,利用勾股定理可求BC;
(2)作![]() 于H,由勾股定理得
于H,由勾股定理得![]() ,整理可得
,整理可得
![]() ,然后在Rt△AHC中有
,然后在Rt△AHC中有![]() ,代入整理好的式子即可证明结论.
,代入整理好的式子即可证明结论.
证明:(1)如图1所示,取AB的中点D,连结CD ,
∵AC=1,AB=2,∴AC=AD=BD=1,
又∵∠A=60°,∴△ACD为等边三角形,
∴AC=AD=DC=BD=1,∠ADC=60°,
∴∠B=∠DCB ,
又∵∠ADC=∠B+∠DCB,
∴∠B=30°,∠ACB=90°,
∴![]() ;
;
(2)如图2所示,作![]() 于H,
于H,
则由勾股定理得:![]() ,
,
∴![]() ,
,
又∵在Rt△AHC中,![]() ,
,
∴![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目