��Ŀ����
����Ŀ��ijУΪ�о�ѧ���Ŀ��మ���������ȡ��������ķ��������Ķ����˶������֡��������ĸ��������������ѧ������Ȥ���ã���������Ľ�����Ƴ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
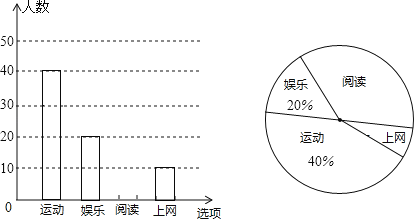
��1��������о��У�һ���������� ��ѧ��������У����![]() ��ѧ��������ȫУ�����˶���ѧ�������� ������
��ѧ��������ȫУ�����˶���ѧ�������� ������
��2����ȫ����ͳ��ͼ���������Ķ�����Բ�Ľ����� ����
��3����ȫУͬѧ�����ѡ��һ��ѧ���μ��ݽ���������Ƶ�ʹ��Ƹ��ʣ���ѡ����ǡ���ǰ����Ķ���ѧ���������� ����
���𰸡���1��![]() ����2����ȫ����ͳ��ͼ�����������Ķ�����Բ�Ľ���108�㣬��3��ѡ����ǡ���ǰ����Ķ���ѧ���ĸ���Ϊ
����2����ȫ����ͳ��ͼ�����������Ķ�����Բ�Ľ���108�㣬��3��ѡ����ǡ���ǰ����Ķ���ѧ���ĸ���Ϊ![]() .
.
��������
��1�����ݰ����˶������İٷֱ��Լ����������������������������������������弴�ɹ���ȫУ�����˶���ѧ��������
��2����������ͳ��ͼ��������Ķ��������Լ��������������Ӷ��ɲ�ȫͼ�Σ�Ȼ����360���������Ķ���������ռ�ٷֱȣ�
��3�����ݰ����Ķ���ѧ��������ռ�İٷֱȼ��ɹ���ѡ����ǡ���ǰ����Ķ���ѧ���ĸ��ʣ�
��1�������˶�������Ϊ![]() ����ռ�ٷֱ�Ϊ
����ռ�ٷֱ�Ϊ![]()
![]() ������������
����������Ϊ��![]() �ˣ�
�ˣ�
�����˶���ѧ��������ռ�İٷֱ�Ϊ![]() ��
��
![]() ȫУ�����˶���ѧ�����У�
ȫУ�����˶���ѧ�����У�![]() �ˣ�
�ˣ�
�ʴ�Ϊ��![]() ��
��
��2���߰�����������Ϊ��![]() �ˣ�
�ˣ�
�మ��������������ռ�ٷֱ�Ϊ![]() ��
��
![]() �����Ķ�����Ϊ��
�����Ķ�����Ϊ��![]() �ˣ�
�ˣ�
��ȫ����ͳ��ͼ����ͼ��ʾ��
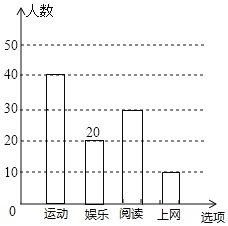
�Ķ�����Բ�Ľ���![]() ��
��
�ʴ�Ϊ��![]() ��
��
��3�������Ķ���ѧ��������ռ�İٷֱ�![]() ��
��
![]() ��Ƶ�ʹ��Ƹ��ʣ���ѡ����ǡ���ǰ����Ķ���ѧ���ĸ���Ϊ
��Ƶ�ʹ��Ƹ��ʣ���ѡ����ǡ���ǰ����Ķ���ѧ���ĸ���Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��