题目内容
如图,点O在ÐAPB的平分在线,圆O与PA相切于点C;

(1) 求证:直线PB与圆O相切;
(2) PO的延长线与圆O交于点E。若圆O的半径为3,PC=4。 求弦CE的长。

(1) 求证:直线PB与圆O相切;
(2) PO的延长线与圆O交于点E。若圆O的半径为3,PC=4。 求弦CE的长。
(1)证明见解析(2) 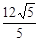
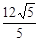
(1) 证明:过点O作OD^PB于点D,连接OC。
∵PA切圆O于点C,
∴OC^PA。
又∵点O在ÐAPB的平分线上,
∴OC=OD。
∴PB与圆O相切。
(2) 解:过点C作CF^OP于点F。
在Rt△PCO中,PC=4,OC=3,
OP=5, =5,
=5,
∵OC´PC=OP´CF=2S△PCO,
∴CF=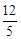 。在Rt△COF中,OF=
。在Rt△COF中,OF= =
=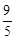 。
。
∴EF=EO+OF=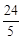 ,∴CE=
,∴CE=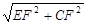 =
=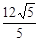 。
。
(1)连接OC,作OD⊥PB于D点.证明OD=OC即可.根据角的平分线性质易证;
(2)设PO交⊙O于F,连接CF.根据勾股定理得PO=5,则PE=8.证明△PCF∽△PEC,得CF:CE=PC:PE=1:2.根据勾股定理求解CE.

∵PA切圆O于点C,
∴OC^PA。
又∵点O在ÐAPB的平分线上,
∴OC=OD。
∴PB与圆O相切。
(2) 解:过点C作CF^OP于点F。
在Rt△PCO中,PC=4,OC=3,
OP=5,
 =5,
=5,∵OC´PC=OP´CF=2S△PCO,
∴CF=
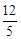 。在Rt△COF中,OF=
。在Rt△COF中,OF= =
=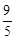 。
。∴EF=EO+OF=
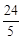 ,∴CE=
,∴CE=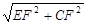 =
=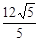 。
。(1)连接OC,作OD⊥PB于D点.证明OD=OC即可.根据角的平分线性质易证;
(2)设PO交⊙O于F,连接CF.根据勾股定理得PO=5,则PE=8.证明△PCF∽△PEC,得CF:CE=PC:PE=1:2.根据勾股定理求解CE.

练习册系列答案
相关题目
 过点A(—1,0),与⊙C相切于点D,求直线
过点A(—1,0),与⊙C相切于点D,求直线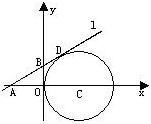
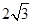 cm
cm cm
cm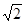 ;
;
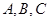 是⊙
是⊙ 上的三点,
上的三点,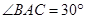 ,则
,则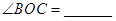 度.
度. 
 是
是 的直径,弦
的直径,弦 ⊥
⊥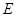 ,
,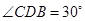 ,
,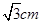 ,则弦
,则弦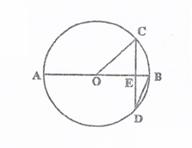
 的半径
的半径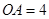 ,
,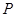 是
是 延长线上一点,过线段
延长线上一点,过线段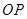 的中点
的中点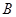 作垂线交
作垂线交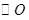 于点
于点 ,射线
,射线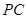 交
交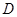 ,联结
,联结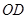 .
.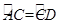 ,求弦
,求弦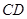 的长.
的长. 上时,设
上时,设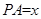 ,
, ,求
,求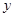 与
与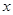 的函数关系式及自变量
的函数关系式及自变量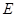 ,射线
,射线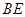 与射线
与射线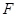 ,当
,当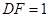 时,请直接写出
时,请直接写出 的值.
的值.