题目内容
已知:半圆 的半径
的半径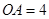 ,
,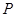 是
是 延长线上一点,过线段
延长线上一点,过线段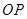 的中点
的中点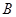 作垂线交
作垂线交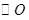 于点
于点 ,射线
,射线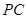 交
交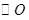 于点
于点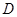 ,联结
,联结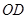 .
.
(1)若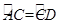 ,求弦
,求弦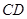 的长.
的长.
(2)若点 在
在 上时,设
上时,设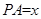 ,
, ,求
,求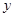 与
与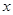 的函数关系式及自变量
的函数关系式及自变量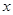 的取值范围;
的取值范围;
(3)设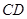 的中点为
的中点为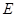 ,射线
,射线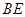 与射线
与射线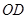 交于点
交于点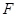 ,当
,当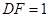 时,请直接写出
时,请直接写出 的值.
的值.
 的半径
的半径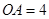 ,
,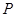 是
是 延长线上一点,过线段
延长线上一点,过线段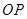 的中点
的中点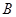 作垂线交
作垂线交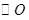 于点
于点 ,射线
,射线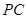 交
交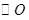 于点
于点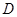 ,联结
,联结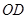 .
.(1)若
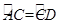 ,求弦
,求弦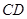 的长.
的长.(2)若点
 在
在 上时,设
上时,设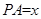 ,
, ,求
,求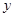 与
与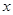 的函数关系式及自变量
的函数关系式及自变量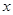 的取值范围;
的取值范围;(3)设
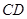 的中点为
的中点为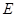 ,射线
,射线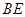 与射线
与射线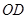 交于点
交于点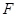 ,当
,当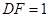 时,请直接写出
时,请直接写出 的值.
的值.
解:(1)连接OC,若当AC=CD时,有∠DOC=∠POC

∵BC垂直平分OP, ∴PC="OC=4," ∴∠P=∠POC=∠DOC
∴△DOC∽△DPO,
∴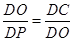 设CD=y, 则16=(y+4)y
设CD=y, 则16=(y+4)y
∴解得
即CD的长为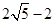
(2)作OE⊥CD,垂足为E,
可得
∵∠P=∠P, ∠PBC=∠PEO=90°∴△PBC∽△PEO
∴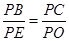 , ∴
, ∴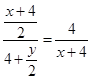
∴ (
(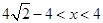 )
)
 (3)若点D在AC外时,
(3)若点D在AC外时,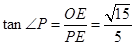
 若点D在AC上时,
若点D在AC上时,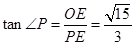

∵BC垂直平分OP, ∴PC="OC=4," ∴∠P=∠POC=∠DOC
∴△DOC∽△DPO,
∴
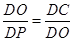 设CD=y, 则16=(y+4)y
设CD=y, 则16=(y+4)y ∴解得

即CD的长为
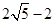
(2)作OE⊥CD,垂足为E,
可得

∵∠P=∠P, ∠PBC=∠PEO=90°∴△PBC∽△PEO
∴
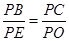 , ∴
, ∴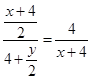
∴
 (
(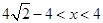 )
)  (3)若点D在AC外时,
(3)若点D在AC外时,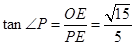
 若点D在AC上时,
若点D在AC上时,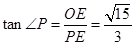
(1)等弧对等角,得出△DOC∽△DPO,可得CD的长;
(2)作OE⊥CD,可得△PBC∽△PEO,由三角形相似比可得
(3)两种情况:点D在AC外,点D在AC上。
(2)作OE⊥CD,可得△PBC∽△PEO,由三角形相似比可得

(3)两种情况:点D在AC外,点D在AC上。

练习册系列答案
相关题目

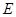 ,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.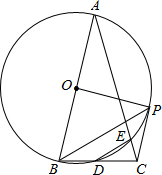


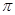 ,则扇形的半径是( )
,则扇形的半径是( )