��Ŀ����
����Ŀ���Ķ����²��ϣ��������Ӧ���⣺
С���ڿ���ѧϰʱ��������һ�����⣺
���壺������κ���y��a1x2+b1x+c1��a1��0��a1��b1��c1�dz�������y��a2x2+b2x+c2��a2��0��a2��b2��c2�dz���������a1+a2��0��b1��b2��c1+c2��0����������������Ϊ����ת������������y��2x2��3x+1����ת������С��������˼���ģ��ɺ���y��2x2��3x+1��֪��a1��2��b1����3��c1��1������a1+a2��0��b1��b2��c1+c2��0�����a2��b2��c2����ȷ�������������ת������
��˼��С���ķ�������������⣺
��1��д������y��x2��4x+3����ת������
��2��������y��5x2+��m��1��x+n��y����5x2��nx��3��Ϊ��ת��������m+n��2020��ֵ��
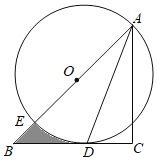
��3����֪����y��2��x��1����x+3����ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����A��B��C����ԭ��ĶԳƵ�ֱ���A1��B1��C1������֤��������A1��B1��C1�Ķ��κ�����y��2��x��1����x+3����Ϊ����ת��������
���𰸡���1��y����x2��4x��3����2��1����3��������
��������
��1���ɶ��κ����Ľ���ʽ�ɵó�a1��b1��c1��ֵ����ϡ���ת�������Ķ�������a2��b2��c2��ֵ�����ʵý⣻
��2���ɺ���y��5x2+��m��1��x+n��y����5x2��nx��3��Ϊ����ת�������������m��n��ֵ��������루m+n��2020����������ۣ�
��3�����ö��κ���ͼ���ϵ�����������������A��B��C�����꣬��϶ԳƵ����ʿ������A1��B1��C1�����꣬�ɵ�A1��B1��C1�����꣬���ý���ʽ���������A1��B1��C1�Ķ��κ�������ʽ�����������Ľ���ʽ���ҳ�a1��b1��c1��a2��b2��c2��ֵ������a1+a2��0��b1��b2��c1+c2��0��֤��������A1��B1��C1�Ķ��κ����뺯��y��2��x��1����x+3����Ϊ����ת��������
�⣺��1����y��x2��4x+3������֪��a1��1��b1����4��c1��3��
��a1+a2��0��b1��b2��c1+c2��0��
��a2����1��b2����4��c2����3��
�ຯ��y��x2��4x+3�ġ���ת������Ϊy����x2��4x��3��
��2����y��5x2+��m��1��x+n��y����5x2��nx��3��Ϊ����ת��������
��![]() ��
��
��ã�![]() ��
��
�ࣨm+n��2020������2+3��2020��1��
��3��֤������x��0ʱ��y��2��x��1����x+3������6��
���C��������0����6����
��y��0ʱ��2��x��1����x+3����0��
��ã�x1��1��x2����3��
���A��������1��0������B����������3��0����
�ߵ�A��B��C����ԭ��ĶԳƵ�ֱ���A1��B1��C1��
��A1����1��0����B1��3��0����C1��0��6����
�����A1��B1��C1�Ķ��κ�������ʽΪy��a��x+1����x��3����
��C1��0��6������y��a��x+1����x��3�����ã�6����3a��
��ã�a����2��
����A1��B1��C1�Ķ��κ�������ʽΪy����2��x+1����x��3������y����2x2+4x+6��
��y��2��x��1����x+3����2x2+4x��6��
��a1��2��b1��4��c1����6��a2����2��b2��4��c2��6��
��a1+a2��2+����2����0��b1��b2��4��c1+c2��6+����6����0��
�ྭ����A1��B1��C1�Ķ��κ����뺯��y��2��x��1����x+3����Ϊ����ת��������

 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д� �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�����Ŀ��ij�̵�ƻ�һ���Թ����ס���������Ʒ��![]() �����ס���������Ʒ�Ľ��ۺ��ۼ����±���ʾ��
�����ס���������Ʒ�Ľ��ۺ��ۼ����±���ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 100 | 80 |
�ۼۣ�Ԫ/���� | 150 | 120 |
�蹺��������Ʒ������Ϊ![]() ����
����
��1��������ɱ�Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() ֮��ĺ�������ʽ��������������Ʒ������������
֮��ĺ�������ʽ��������������Ʒ������������![]() ��������ͽ����ɱ��Ƕ���Ԫ��
��������ͽ����ɱ��Ƕ���Ԫ��
��2�������˽����ɱ�����Ҫ֧���˷Ѻ�����Ա�����ʹ�![]() Ԫ��Ϊ��������ʽ𣬸��̵�����Լ�����Ʒ���н������ۣ�ÿ��������Ʒ����
Ԫ��Ϊ��������ʽ𣬸��̵�����Լ�����Ʒ���н������ۣ�ÿ��������Ʒ����![]() Ԫ
Ԫ![]() ��������Ʒ�ۼ۲��䣬��������ס���������Ʒ��õ�������Ϊ
��������Ʒ�ۼ۲��䣬��������ס���������Ʒ��õ�������Ϊ![]() Ԫ��
Ԫ��
��ÿ��������Ʒ�������� Ԫ���ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
����![]() ����
����![]() �ĺ�������ʽ
�ĺ�������ʽ
�۵�![]() ʱ���������
ʱ���������![]() ��ȡֵ��Χ��˵�����̵깺��������Ʒ���ټ�ʱ����õ����������
��ȡֵ��Χ��˵�����̵깺��������Ʒ���ټ�ʱ����õ����������
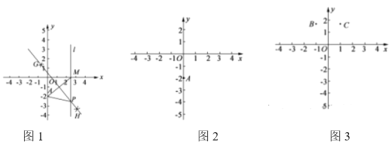
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A��������![]() ����x������ȡһ��M������AM���ֱ��Ե�A�͵�MΪԲ�ģ�����
����x������ȡһ��M������AM���ֱ��Ե�A�͵�MΪԲ�ģ�����![]() �ij�Ϊ�뾶�����������ཻ��G��H���㣬��ֱ��GH������M��x��Ĵ���l��ֱ��GH�ڵ�P���������ϲ���������������⣮
�ij�Ϊ�뾶�����������ཻ��G��H���㣬��ֱ��GH������M��x��Ĵ���l��ֱ��GH�ڵ�P���������ϲ���������������⣮
̽����
��1���߶�PA��PM��������ϵΪ________��������Ϊ��________________��
��2����x���϶�θı��M��λ�ã���������ͼ�����õ���Ӧ��P�����꣬��������б���
M������ | �� |
|
|
|
| �� |
P������ | �� |
|
| �� |
���룺
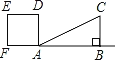
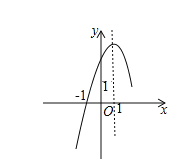
��3�����������������P������꣬����Щ����ƽ����������ͼ2�������������۲컭��������L����������L����״��________��
��֤��
��4�����P��������![]() ������ͼ1���߶�PA��PM�Ĺ�ϵ�����y����x�ĺ�������ʽ��
������ͼ1���߶�PA��PM�Ĺ�ϵ�����y����x�ĺ�������ʽ��
Ӧ�ã�
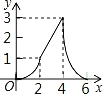
��5����ͼ3����![]() ��
��![]() �����D��������
�����D��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��