题目内容
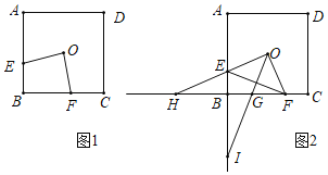
【题目】如图1,点![]() 是正方形
是正方形![]() 的中心,点
的中心,点![]() 是
是![]() 边上一动点,在
边上一动点,在![]() 上截取
上截取![]() ,连结
,连结![]() ,
,![]() .初步探究:在点
.初步探究:在点![]() 的运动过程中:
的运动过程中:
(1)猜想线段![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
深入探究:
(2)如图2,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .交
.交![]() 的延长线于点
的延长线于点![]() .延长
.延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
①直接写出![]() 的度数.
的度数.
②若![]() ,请探究
,请探究![]() 的值是否为定值,若是,请求出其值;反之,请说明理由
的值是否为定值,若是,请求出其值;反之,请说明理由
【答案】(1)EO⊥FO,EO=FO;理由见解析;(2)①![]() ;②
;②![]() =2
=2
【解析】
(1)由正方形的性质可得BO=CO,∠ABO=∠ACB=45°,∠BOC=90°,由“SAS”可证△BEO≌△CFO,可得OE=OF,∠BOE=∠COF,可证EO⊥FO;
(2)①由等腰直角三角形的性质可得∠EOG的度数;
②由∠EOF=∠ABF=90°,可得点E,点O,点F,点B四点共圆,可得∠EOB=∠BFE,通过证明△BOH∽△BIO,可得![]() ,即可得结论.
,即可得结论.
解:(1)OE=OF,OE⊥OF,连接AC,BD,
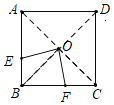
∵点O是正方形ABCD的中心
∴点O是AC,BD的交点
∴BO=CO,∠ABO=∠ACB=45°,∠BOC=90°
∵CF=BE,∠ABO=∠ACB,BO=CO,
∴△BEO≌△CFO(SAS)
∴OE=OF,∠BOE=∠COF
∵∠COF+∠BOF=90°,
∴∠BOE+∠BOF=90°
∴∠EOF=90°,
∴EO⊥FO.
(2)
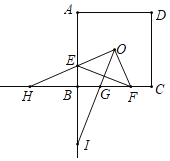
①∵OE=OF,OE⊥OF,
∴△EOF是等腰直角三角形,OG⊥EF
∴∠EOG=45°
②BHBI的值是定值,
理由如下:
如图,连接DB,
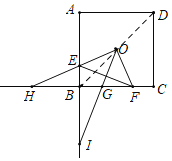
∵AB=BC=CD=2
∴BD=2![]() ,
,
∴BO=![]()
∵∠AOB=∠COB=45°,∠HBE=∠GBI=90°
∴∠HBO=∠IBO=135°
∵∠EOF=∠ABF=90°
∴点E,点O,点F,点B四点共圆
∴∠EOB=∠BFE,
∵EF⊥OI,AB⊥HF
∴∠BEF+∠BFE=90°,∠BEF+∠EIO=90°
∴∠BFE=∠BIO,
∴∠BOE=∠BIO,且∠HBO=∠IBO
∴△BOH∽△BIO
∴![]()
∴BHBI=BO2=2