Question

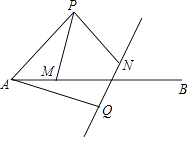
【题目】如图，在△ABC中，∠B=45°，∠ACB=30°，点D是BC上一点，连接AD，过点A作AG⊥AD，点F在线段AG上，延长DA至点E，使AE=AF，连接EG，CG，DF，若EG=DF，点G在AC的垂直平分线上，则 的值为

Answer 1

【答案】
【解析】解：过点A作AH⊥BC于点H，过点G作GK⊥BC于K，过点A作AL⊥GK于点L，取AC中点M，连接GM．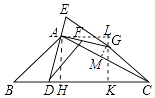
∵AG⊥DE，
∴∠DAF=∠EAG=90°
在Rt△ADF和Rt△AGE中，
，
∴Rt△ADF≌Rt△AGE，
∴AD=AG，
∵∠AHK=∠ALK=∠LKH=90°，
∴四边形AHKL是矩形，
∴∠DAG=∠HAL=90°，
∴∠DAH=∠GAL，∵∠AHD=∠ALG=90°，
∴△ADH≌△AGL，
∴AH=AL，
在Rt△ACH中，∵∠ACH=30°，
∴AH=AL= AC=AM，
∵AG=AG，∠ALG=∠AMG=90°，
∴Rt△AGM≌Rt△AGL，
∴∠GAL=∠GAM，
∵AL∥BC，
∴∠CAL=∠ACH=30°，
∴∠GAL=∠GAM=15°，
∴∠DAH=∠GAL=15°，
∴∠CAD=∠CDA=75°，
∴AC=AD，设AH=a，则CD=AC=2a，CH= a，
∴LG=DH=CD﹣CH=2a﹣ a，
∴GK=LK﹣LG=（ ﹣1）a，
∵GA=GC，
∴∠GAC=∠GCA=15°，
∴∠GCK=45°，
∴CG= KG=（ ﹣ ）a，∵AB= AH= a，
∴ = = ．
所以答案是 ．