题目内容
【题目】（探究）
（1）观察下列算式，并完成填空：
1=12
1+3=4=22；
1+3+5=9=32；
1+3+5+7=16=42；
1+3+5+…+（2n-1）=______．（n是正整数）
（2）如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案，图案中央是一块正六边形地板砖，周围是正方形和正三角形的地板砖．从里向外第一层包括6块正方形和6块正三角形地板砖；第二层包括6块正方形和18块正三角形地板砖；以此递推．
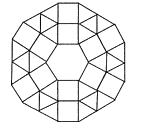
①第3层中分别含有______块正方形和______块正三角形地板砖；
②第n层中含有______块正三角形地板砖（用含n的代数式表示）．
（应用）
该市打算在一个新建广场中央，采用如图样式的图案铺设地面，现有1块正六边形、150块正方形和420块正三角形地板砖，问：铺设这样的图案，最多能铺多少层？请说明理由．
【答案】【探究】n2；（2）① 6，30；②6（2n-1）或12n-6；【应用】铺设这样的图案，最多能铺8层，理由见解析
【解析】
一．探究（1）观察算式规律，1+3+5+…+（2n-1）=n2；
（2）①第一层6块正方形和6块正三角形地板砖，第二层6块正方形和6+12=18块正三角形地板砖，第三层6块正方形和18+12=30块正三角形地板砖；
②第一层6=6×1=6×（2×1-1）块正三角形地板砖，第二层18=6×3=6×（2×2-1）块正三角形地板砖，第三层30=6×5=6×（2×3-1）块正三角形地板砖，第n层6=6×1=6（2n-1）块正三角形地板砖，
二．应用
150块正方形地板砖可以铺设这样的图案150÷6=25（层），铺设n层需要正三角形地板砖的数量为：6[1+3+5+…+（2n-1）]=6n2，6n2=420，n2=70，n=
，8＜n＜9，所以420块正三角形地板砖最多可以铺设这样的图案8层．因此铺设这样的图案，最多能铺8层．
解：一.探究
（1）观察算式规律，1+3+5+…+（2n-1）=n2，
故答案为n2；
（2）①∵第一层包括6块正方形和6块正三角形地板砖，
第二层包括6块正方形和6+12=18块正三角形地板砖，
∴第三层包括6块正方形和18+12=30块正三角形地板砖，
故答案为6，30；
②∵第一层6=6×1=6×（2×1-1）块正三角形地板砖，
第二层18=6×3=6×（2×2-1）块正三角形地板砖，
第三层30=6×5=6×（2×3-1）块正三角形地板砖，
∴第n层6=6×1=6（2n-1）块正三角形地板砖，
故答案为6（2n-1）或12n-6．
二．应用
铺设这样的图案，最多能铺8层．
理由如下：
∵150÷6=25（层），
∴150块正方形地板砖可以铺设这样的图案25层；
∵铺设n层需要正三角形地板砖的数量为：6[1+3+5+…+（2n-1）]=6n2，
∴6n2=420，n2=70，n=．
又∵8＜ ＜9，即8＜n＜9，
∴420块正三角形地板砖最多可以铺设这样的图案8层．
∴铺设这样的图案，最多能铺8层．
