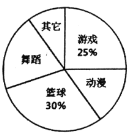
题目内容
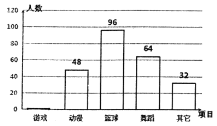
【题目】某校为了解禁毒知识宣传的效果，针对全校学生进行了一次测试，并随机抽取 了部分学生的测试成绩(满分100分，最低分为60分，80分及以上为优秀)，统计后绘制成如下不完整的
请根据以上信息，解答下列问题：
（1）表中
__________，
_________；
（2）请补全频数分布直方图；
（3）若该校有学生2100人，试估计分数达到优秀的有多少人；
（4）学校准备从得分最高的5名学生(3男2女)中，随机挑选2名学生去参加市里举办的禁毒知识竞赛．小明说：“因为男生人数是女生人数的
倍，所以选中的2名学生都是男生的概率是选中的2名学生都是女生的概率的倍．”他的说法正确吗？请判断并说明理由．
【答案】（1）120，0.1；（2）见解析；（3）若该校有学生2100人，试估计分数达到优秀的有1050人；（4）不正确，理由见解析
【解析】
（1）根据70≤x＜80的频数及频率即可求出a的值，根据90≤x≤100的频数及a的值即可求出b；
（2）计算出80≤x＜90的频数即可补全直方图；
（3）根据80≤x＜90以及90≤x≤100的频率即可求出达到优秀的人数；
（4）通过列表法，列出所有情况，共有20种等可能的结果，再分别计算概率即可判断．
解：（1）
（人）
∵
故答案为：120，
；
（2）80≤x＜90的频数为120×0.4=48（人）
∴补全频数分布直方图如下：
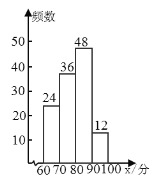
（3）
（人）
故若该校有学生2100人，试估计分数达到优秀的有1050人．
（4）不正确．理由：根据题意，列表如下：
由上表可知，共有20种等可能的结果，其中选中的2名学生都是男生的结果有6种，故其概率为
；选中的2名学生都是女生的结果有2种，故其概率为
，
，
故小明的说法不正确．
【题目】某大学生利用暑假40天社会实践参与了某公司旗下一家加盟店经营，了解到一种成本为20元/件的新型商品在第
天销售的相关信息如下表所示：
销售量 |
|
销售单价 | 当 当 |
（1）请计算第几天该商品的销售单价为35元/件；
（2）这40天中该加盟店第几天获得的利润最大？最大利润是多少？
（3）在实际销售的前20天中，公司为鼓励加盟店接收大学生参加实践活动决定每销售一件商品就发给该加盟店
元奖励，通过该加盟店的销售记录发现，前10天中，每天获得奖励后的利润随时间（天）的增大而增大，求
的取值范围．
