题目内容
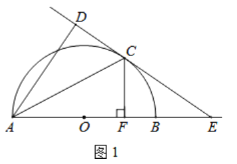
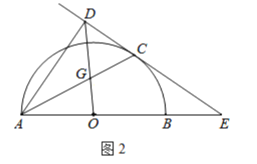
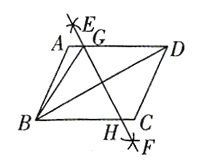
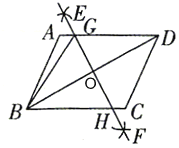
【题目】如图.已知四边形ABCD是平行四边形,结合作图痕迹,下列说法不正确的是( )
A.![]() 与
与![]() 垂直
垂直
B.![]()
C.![]() 平分
平分![]()
D.若![]() 的周长为4,则平行四边形
的周长为4,则平行四边形![]() 的周长为8
的周长为8
【答案】C
【解析】
设EF与BD的交点为点O,由作图痕迹可得,直线EF是BD的垂直平分线,故A正确;证明△DOG≌△BOH,得到GD=HB,进而可得B正确;求出![]() 平分∠GBC可得C错误;根据AB+AG+BG=AB+AG+GD=AB+AD=4,可得平行四边形
平分∠GBC可得C错误;根据AB+AG+BG=AB+AG+GD=AB+AD=4,可得平行四边形![]() 的周长为8,即D正确.
的周长为8,即D正确.
解:设EF与BD的交点为点O,由作图痕迹可得,直线EF是BD的垂直平分线,
∴![]() 与
与![]() 垂直,A选项说法正确;
垂直,A选项说法正确;
∵AD∥BC,EF是BD的垂直平分线,
∴∠GDB=∠DBH,DO=BO,
又∵∠GOD=∠BOH,
∴△DOG≌△BOH,
∴GD=HB,
∴![]() ,B选项说法正确;
,B选项说法正确;
∵EF垂直平分BD,
∴BG=DG,
∴∠GBD=∠GDB,
又∵∠GDB=∠DBH,
∴∠GBD=∠DBH,
∴![]() 平分∠GBC,
平分∠GBC,
∵∠ABC=∠ADC≠∠GBC,
∴C选项说法错误;
∵![]() 的周长为4,BG=GD,
的周长为4,BG=GD,
∴AB+AG+BG=AB+AG+GD=AB+AD=4,
∴平行四边形![]() 的周长=2×(AB+ AD)=8,D选项说法正确,
的周长=2×(AB+ AD)=8,D选项说法正确,
故选:C.

 名校课堂系列答案
名校课堂系列答案【题目】某企业对一种设备进行升级改造,并在一定时间内进行生产营销,设改造设备的台数为x,现有甲、乙两种改造方案.
甲方案:升级后每台设备的生产营销利润为4000元,但改造支出费用![]() 由材料费和施工费以及其他费用三部分组成,其中材料费与x的平方成正比,施工费与x成正比,其他费用为2500元,(利润=生产营销利润-改造支出费用).设甲方案的利润为
由材料费和施工费以及其他费用三部分组成,其中材料费与x的平方成正比,施工费与x成正比,其他费用为2500元,(利润=生产营销利润-改造支出费用).设甲方案的利润为![]() (元),经过统计,得到如下数据:
(元),经过统计,得到如下数据:
改造设备台数x(台) | 20 | 40 |
利润 | 9500 | 5500 |
乙方案:升级后每台设备的生产营销利润为3500元,但改造支出费用![]() 与x之间满足函数关系式:
与x之间满足函数关系式:![]() (a为常数,
(a为常数,![]() ),且在使用过程中一共还需支出维护费用
),且在使用过程中一共还需支出维护费用![]() ,(利润=生产营销利润-改造支出费用-维护费用).设乙方案的利润为
,(利润=生产营销利润-改造支出费用-维护费用).设乙方案的利润为![]() (元).
(元).
(1)分别求出![]() ,
,![]() 与x的函数关系式;
与x的函数关系式;
(2)若![]() ,
,![]() 的最大值相等,求a的值;
的最大值相等,求a的值;
(3)如果要将30台设备升级改造,请你帮助决策,该企业应选哪种方案,所获得的利润较大.