题目内容
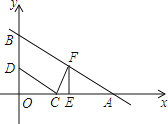
【题目】如图,在平面直角坐标系中,一次函数图象与x轴,y轴分别交于点A(8,0),B(0,4),点C的坐标为(3,0),动点D是射线BO上一个动点,连结CD,过点C作CD⊥FC,交一次函数图象于点F.
(1)求这个一次函数的解析式;
(2)过点F作FE⊥x轴,垂足为点E,当△OCD与△EFC全等时,求出满足条件的点F的坐标;
(3)点D在运动过程中,是否存在使△ACF是等腰三角形?若存在请求出点F的坐标;不存在,请说明理由.
【答案】(1)y=-![]() x+4;(2)(2,3);(3)存在,(0,4)或(8-2
x+4;(2)(2,3);(3)存在,(0,4)或(8-2![]() ,
,![]() )
)
【解析】
(1)利用待定系数法,由点A(8,0),B(0,4)即可求出直线解析式.
(2)△OCD与△EFC全等分为两种情况,由全等得出线段EF或CE长度,进而求出点F的横坐标或纵坐标,代入直线解析式就可以求出点F的坐标.
(3)△ACF是等腰三角形,可以分三种情况讨论,根据等腰三角形性质求出F点的坐标.
(1)设一次函数解析式为y=kx+b(k≠0,k、b为常数),
将点A(8,0),B(0,4)代入得:![]() ,
,
解得:k=-![]() ,b=4.
,b=4.
故一次函数解析式为:y=-![]() x+4.
x+4.
(2)∵△OCD与△EFC全等,
∴可以分两种情况:△OCD≌△EFC或△OCD≌△ECF,
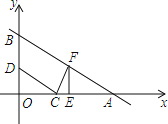
①当△OCD≌△EFC时,
OC=EF=3,
∴点F纵坐标为3,
将y=3代入直线解析式得:x=2,
∴F(2,3).
②当△OCD≌△ECF,
OC=EC=3,
∴点F横坐标为6,
将x=6代入直线解析式得:y=1,
∴F(6,1)(不合题意舍弃).
∴F点坐标为:(2,3)
(3)存在.
△ACF是等腰三角形,
①当CF=AF时,
根据等腰三角形三线合一性质,得点E为AC中点,
AC=5,CE=![]() ,
,
∴OE=![]() ,即F点横坐标为
,即F点横坐标为![]() ,
,
将x=![]() 代入一次函数得y=
代入一次函数得y=![]() ,
,
∴F(![]() ).
).
此时点D会出现在点B的上方,与题意不符,舍去;
②当AF=AC时,OB=4,OA=8,
AB=4![]() .
.
∵EF∥OB,
∴△AEF∽△AOB.
∴![]() ,
,
解得:EF=![]() .
.
将y=![]() 代入直线解析式,得:x=8-2
代入直线解析式,得:x=8-2![]() ,
,
∴F(8-2![]() ,
,![]() ).
).
③当CF=AC=5时,
∵OC=3,OB=4,
∴BC=5,
此时,CB=CF,点F与点B重合,
∴F(0,4) ,
∴点F坐标为:(0,4)或(8-2![]() ,
,![]() ).
).

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】体育李老师为了解九年级女生体质健康的变化情况,本学期从九年级全体90名女生中随机抽取15名女生进行体质测试,并调取该15名女生上学期的体质测试成绩进行对比,李老师对两次数据(成绩)进行整理、描述和分析.下面给出了部分信息.
![]() .两次测试成绩(百分制)的频数分布直方图如下(数据分组:
.两次测试成绩(百分制)的频数分布直方图如下(数据分组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
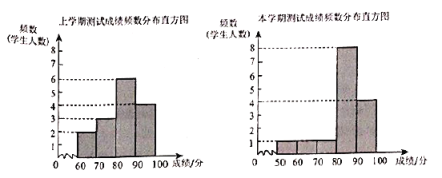
![]() .上学期测试成绩在
.上学期测试成绩在![]() 的是:80 81 83 84 84 88
的是:80 81 83 84 84 88
![]() .两个学期测试成绩的平均数、中位数、众数如下:
.两个学期测试成绩的平均数、中位数、众数如下:
学期 | 平均数 | 中位数 | 众数 |
上学期 | 82.9 |
| 84 |
本学期 | 83 | 86 | 86 |
根据以上信息,回答下列问题:
(1)表中![]() 的值是______;
的值是______;
(2)体育李老师计划根据本学期统计数据安排80分以下(不含80分)的同学参加体质加强训练项目,则九年级约有______名女生参加此项目;
(3)分析这15名女生从上学期到本学期体质健康变化的总体情况.(从两个方面进行分析)