题目内容
【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC。
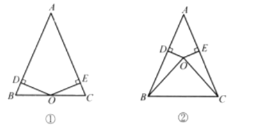
(1)如图①,若点O在BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,上题的结论还成立吗?为什么?
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示。
【答案】(1)详见解析;(2)成立,证明详见解析;(3)不一定成立,图详见解析.
【解析】
(1)根据已知条件易证Rt△BOD≌Rt△COE,即可得∠B=∠C,根据等角对等边的性质,即可证得AB=AC;(2)结论成立,根据已知条件易证得Rt△BOD≌Rt△COE,然后又由OB=OC,根据等边对等角的性质,易证得∠ABC=∠ACB,根据等角对等边的性质可得AB=AC;(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时,类比(1)的方法可证AB=AC;当∠A的平分线所在直线与边BC的垂直平分线不重合时,过点O作OD⊥AB于D,作OE⊥AC的延长线于点E,连接OA,由题意可得OD=OE,根据角平分线的判定定理可得点O在∠BAC的平分线上,易证△ADO≌△AEO,可得AD=AE,由此可得AB≠AC.
(1)由题意可得,OD=OE,∠ODB=∠OEC=90°,
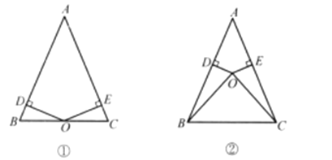
在Rt△BOD和Rt△COE中,
∵![]() ,
,
∴Rt△BOD≌Rt△COE(HL),
∴∠B=∠C,
∴AB=AC;
(2)点O在△ABC的内部,上题的结论成立,理由如下:
由题意可得,OD=OE,∠ODB=∠OEC=90°,
在Rt△BOD和Rt△COE中,
∵![]() ,
,
∴Rt△BOD≌Rt△COE(HL),
∴∠DBO=∠ECO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.
证明:①当∠A的平分线所在直线与边BC的垂直平分线重合时(如图3),过点O作OD⊥AB于D,作OE⊥AC的延长线于点E,

则OD=OE,∠ODB=∠OEC=90°,
在Rt△BOD和Rt△COE中,
∵![]() ,
,
∴Rt△BOD≌Rt△COE(HL),
∴∠DBO=∠ECO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠DBC=∠ECB,
∴∠ABC=∠ACB,
∴AB=AC.
②当∠A的平分线所在直线与边BC的垂直平分线不重合时(如图4),
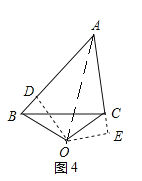
过点O作OD⊥AB于D,作OE⊥AC的延长线于点E,连接OA,由题意可得OD=OE,根据角平分线的判定定理可得点O在∠BAC的平分线上,易证△ADO≌△AEO,可得AD=AE,由此可得AB≠AC.

 阅读快车系列答案
阅读快车系列答案【题目】如图是用长度相等的小棒按一定规律摆成的一组图案

(1)填写下表:
图形序号 | ① | ② | ③ | …… | ⑧ |
每个图案中小棒的数量 | 6 | 11 | …… |
(2)请填写出第![]() 个图案中小棒的数量(用含
个图案中小棒的数量(用含![]() 的代数式表示);
的代数式表示);
(3)第30个图案中小棒有多少根?