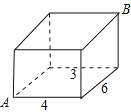
题目内容
【题目】直线y=﹣![]() x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣
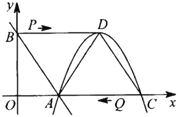
x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣![]() x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.
x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.
(1)直接写出抛物线的解析式和点A,C,D的坐标;
(2)动点P在BD上以每秒2个单位长的速度由点B向点D运动,同时动点Q在CA上以每秒3个单位长的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.
①当∠DPE=∠CAD时,求t的值;
②过点E作EM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB或AD于点N,当PN=EM时,求t的值.
【答案】(1)点A(2,0),点C(6,0),点D(4,3),(2)①![]() 秒;(2)t=(1﹣
秒;(2)t=(1﹣![]() )秒或t=
)秒或t=![]() 秒.
秒.
【解析】(1)先由直线解析式求得点A、B坐标,将点A坐标代入抛物线解析式求得m的值,从而得出答案;
(2)①由(1)知BD=AC、BD//OC,根据AB=AD=![]() 证四边形ABPQ是平行四边形得AQ=BP,即2t=4-3t,解之即可;
证四边形ABPQ是平行四边形得AQ=BP,即2t=4-3t,解之即可;
②分点N在AB上和点N在AD上两种情况分别求解.
(1)在![]() 中,令
中,令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
∴点![]() 、点
、点![]() ,
,
将点![]() 代入抛物线解析式,得:
代入抛物线解析式,得:![]() ,
,
解得:![]() ,
,
所以抛物线解析式为![]() ,
,
∵y![]() ,
,
∴点![]() ,对称轴为
,对称轴为![]() ,
,
∴点C坐标为![]() ;
;
(2)如图1,
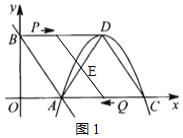
由(1)知![]() ,
,
根据![]() ,得:
,得:![]() ,
,
①∵![]() 、
、![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 、
、![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形ABPQ是平行四边形,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
即当![]() 时,
时,![]() 秒;
秒;
②![]() Ⅰ
Ⅰ![]() 当点N在AB上时,
当点N在AB上时,![]() ,即
,即![]() ,
,
连接NE,延长PN交x轴于点F,延长ME交x轴于点H,
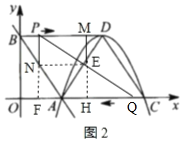
∵![]() 、
、![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() 、
、![]() ,
,![]() ,
,
∴![]() ,
,
∵点N在直线![]() 上,
上,
∴点N的坐标为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 、
、![]() ,
,
∴直线AD解析式为![]() ,
,
∵点E在直线![]() 上,
上,
∴点E的坐标为![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() 舍
舍![]() 或
或![]() ;
;
![]() Ⅱ
Ⅱ![]() 当点N在AD上时,
当点N在AD上时,![]() ,即
,即![]() ,
,
∵![]() ,
,
∴点E、N重合,此时![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
综上所述,当![]() 时,
时,![]() 秒或
秒或![]() 秒
秒![]()

【题目】平价商场经销的甲、乙两种商品,甲种商品每件售价98元,利润率为40%;乙种商品每件进价80元,售价128元.
(1)甲种商品每件进价为 元,每件乙种商品利润率为 .
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为3800元,求购进甲、乙两种商品各多少件?
(3)在“元且“期间,该商场只对乙种商品进行如下的优惠促销活动:按下表优惠条件,
打折前一次性购物总金额 | 优惠措施 |
少于等于480元 | 不优惠 |
超过480元,但不超过680元 | 其中480元不打折,超过480元的部分给予6折优惠 |
超过680元 | 按购物总额给予7.5折优惠 |
若小华一次性购买乙种商品实际付款576元,求小华在该商场购买乙种商品多少件?