题目内容
我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2•i=(﹣1)•i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n•i=(i4)n•i=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为【 】
| A.0 | B.1 | C.﹣1 | D.i |
D。
由题意得,i1=i,i2=﹣1,i3=i2•i=(﹣1)•i=﹣i,i4=(i2)2=(﹣1)2=1,i5=i4•i=i,i6=i5•i=﹣1,
可发现4次一循环,一个循环内的和为0,
∵2013÷4=503…1,∴i+i2+i3+i4+…+i2012+i2013=i。
故选D。
可发现4次一循环,一个循环内的和为0,
∵2013÷4=503…1,∴i+i2+i3+i4+…+i2012+i2013=i。
故选D。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ;②、
;②、
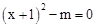 有两个实数根,则m的取值范围是
有两个实数根,则m的取值范围是



 有两个不相等的实数根,则k的取值范围是【 】
有两个不相等的实数根,则k的取值范围是【 】 售价下调到每斤是5元,下列所列方程中正确的是【 】
售价下调到每斤是5元,下列所列方程中正确的是【 】



 有两个不相等的实数根,则m的取值范围在数轴上表示正确的是
有两个不相等的实数根,则m的取值范围在数轴上表示正确的是



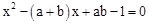 ,x1、x2是此方程的两个实数根,现给出三个结论:①x1≠x2;②x1x2<ab;③
,x1、x2是此方程的两个实数根,现给出三个结论:①x1≠x2;②x1x2<ab;③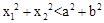 .则正确结论的序号是 .(填上你认为正确结论的所有序号)
.则正确结论的序号是 .(填上你认为正确结论的所有序号)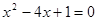 ;(2)
;(2)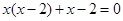 .
.