Question

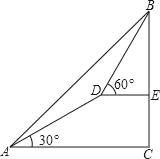
【题目】如图，矩形ABCD的对角线AC，BD交于点O，以OC，OD为邻边作平行四边形OCED，连接OE．

（1）求证：四边形OBCE是平行四边形；

（2）连接BE交AC于点F．若AB=2，∠AOB=60°，求BF的长．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）由四边形ABCD是矩形，得到四边形OCED为菱形，易证四边形OBCE为平行四边形.

（2）过B作BH⊥AC于H，易证：OH=OF==2,可得BF.

（1）证明：∵四边形ABCD是矩形，

∴OA＝OB＝OC＝OD，

∵四边形OCED是平行四边形，

∴四边形OCED为菱形，

∴CE∥OB，CE＝OB，

∴四边形OBCE为平行四边形；

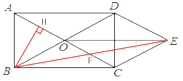
（2）解：过B作BH⊥AC于H，

∵四边形ABCD是矩形，

∴AO=BO，

又∠AOB是60°，

∴△AOB是等边三角形，

∵BH⊥AO，∴AH=HO.

∵四边形OCED是平行四边形，

∴CE∥OD，且CE=OD，

∴CE∥OB，且CE=OB，

∴OF=FC.

又AO=OC，

∴OH=OF==2,

在直角三角形BHF中，BH=

所以