题目内容
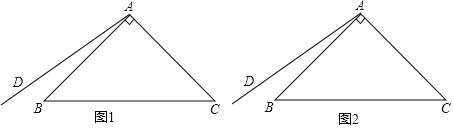
【题目】已知△ABC中,∠BAC=90°,AB=AC,在△ABC外侧作射线AD,点B关于射线AD的对称点为E,连接CE,CE交射线AD与点F.
(1)依题意补全如图.
(2)设∠BAD=α,若0°<α<45°,求∠AEC的大小(用含α的代数式表示).
(3)如图,0°<∠BAD<45°,用等式表示线段EC,FC与EB之间的数量关系.
【答案】(1)补图见解析;(2)∠AEC==45°-α.证明见解析;(3)EB=![]() (EC-FC),证明见解析.
(EC-FC),证明见解析.
【解析】
(1)根据要求画出图形即可.
(2)首先证明∠EAC=90°+2α,理由等腰三角形的性质即可解决问题.
(3)结论:EB=![]() (EC-FC).想办法证明△EFB是等腰直角三角形即可解决问题.
(EC-FC).想办法证明△EFB是等腰直角三角形即可解决问题.
(1)所画图形,如图所示.
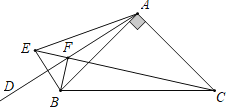
(2)∵点B关于射线AD的对称点为E,
∴∠EAD=∠BAD=α,
∵∠BAC=90°,
∴∠EAC=90°+2α,
∵AE=AB=AC,
∴∠AEC=![]() (180°-90°-2α)=45°-α.
(180°-90°-2α)=45°-α.
(3)结论:结论:EB=![]() (EC-FC).
(EC-FC).
理由:∵∠EFD=∠AEC+∠AEF=45°-α+α=45°,
∵AD垂直平分线段BE,
∴∠BFD=∠EFD=45°,
∴∠EFB=90°,∵FE=FB,
∴△EFB是等腰直角三角形,
∴EC-CF=EF=![]() EB,
EB,
∴EB=![]() (EC-FC).
(EC-FC).

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目