题目内容
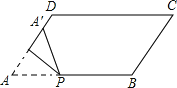
【题目】如图,平行四边形纸片ABCD,CD=5,BC=2,∠A=60°,将纸片折叠,使点A落在射线AD上(记为点A′),折痕与AB交于点P,设AP的长为x,折叠后纸片重叠部分的面积为y,可以表示y与x之间关系的大致图象是( )
A. 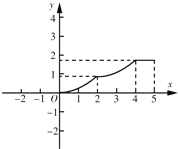 B.
B. 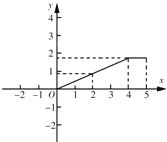
C. 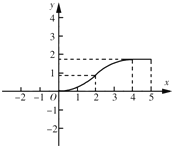 D.
D. 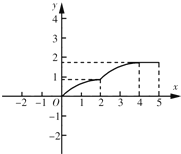
【答案】C
【解析】
根据题意结合等边三角形的性质得出当0≤x≤2时,当2≤x≤4时,y与x的函数解析式,进而求出符合题意的图象.
如图1,当0≤x≤2时,
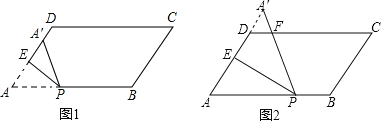
∵∠A=60°,AP=A′P,
∴△APA′是等边三角形,
∴设AP的长为x,则EP=![]() x,A′E=
x,A′E=![]() x,
x,
折叠后纸片重叠部分的面积为y=![]() ×
×![]() x×
x×![]() x=
x=![]() x2,
x2,
如图2,当2≤x≤4时,可得△APA′是等边三角形,
设AP的长为x,则EP=![]() x,A′D=x-2,
x,A′D=x-2,
折叠后纸片重叠部分的面积为y=![]() x2-
x2-![]() ×(x-2)×
×(x-2)×![]() (x-2)=-
(x-2)=-![]() x2+
x2+![]() x-
x-![]() ,
,
当4≤x≤5时,折叠后纸片重叠部分的面积为y是恒定值,
故符合题意的图象是C.
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目