题目内容
【题目】如图，把ΔABC剪成三部分，边AB，BC，AC放在同一直线上，点O都落在直线MN上，直线MN∥AB．在ΔABC中，若∠AOB=125°，则∠ACB的度数为（ ）
A. 70°B. 65°C. 60°D. 85°
【答案】A
【解析】
利用平行线间的距离处处相等，可知点O到BC、AC、AB的距离相等，得出O为三条角平分线的交点，根据三角形内角和定理和角平分线的定义即可得出结论．
如图1，过点O作OD⊥BC于D，OE⊥AC于E，OF⊥AB于F．
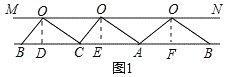
∵MN∥AB，∴OD=OE=OF（平行线间的距离处处相等）．
如图2：过点O作OD'⊥BC于D'，作OE'⊥AC于E'，作OF'⊥AB于F'．
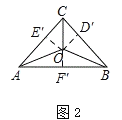
由题意可知：OD=OD'，OE=OE'，OF=OF'，∴OD'=OE'=OF'，∴图2中的点O是三角形三个内角的平分线的交点．
∵∠AOB=125°，∴∠OAB+∠OBA=180°－125°=55°，∴∠CAB+∠CBA=2×55°=110°，∴∠ACB=180°－110°=70°．
故选A．
【题目】 “赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
请结合图表完成下列各题：
（1）①表中a的值为 ，中位数在第 组；
②频数分布直方图补充完整；
（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．
组别 | 成绩x分 | 频数（人数） |
第1组 | 50≤x＜60 | 6 |
第2组 | 60≤x＜70 | 8 |
第3组 | 70≤x＜80 | 14 |
第4组 | 80≤x＜90 | a |
第5组 | 90≤x＜100 | 10 |
【题目】某学习小组在研究函数y=
x3﹣2x的图象与性质时，已列表、描点并画出了图象的一部分．
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
（1）请补全函数图象；
（2）方程
x3﹣2x=﹣2实数根的个数为 ；
（3）观察图象，写出该函数的两条性质．
