题目内容
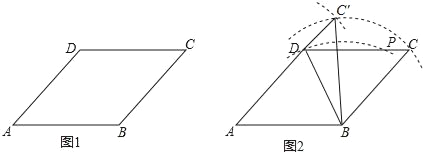
【题目】为判断命题“有三条边相等且一组对角相等的四边形是菱形”的真假,数学课上,老师给出菱形ABCD如图1,并作出了一个四边形ABC′D.具体作图过程如下:
如图2,在菱形ABCD中,
①连接BD,以点B为圆心,以BD的长为半径作圆弧,交CD于点P;
②分别以B、D为圆心,以BC、PC的长为半径作圆弧,两弧交于点C′.
③连接BC′、DC′,得四边形ABC′D.
依据上述作图过程,解决以下问题:
(1)求证:∠A=∠C′;AD=BC′.
(2)根据作图过程和(1)中的结论,说明命题“有三条边相等且有一组对顶角相等的四边形是菱形”是 命题.(填写“真”或“假”)
【答案】(1)见解析;(2)真
【解析】
(1)连接BP,由菱形的性质得出AD=BC,∠A=∠BCD,根据题意得出BC=B′C,BD=BP,DC′=PC,得出AD=BC′,由SSS证明△BPC≌△BDC′,得出对应角相等∠BCD=∠C′,即可得出∠A=∠C′;
(2)由(1)可知命题“有三条边相等且有一组对顶角相等的四边形是菱形”是真命题.
证明:连接BP,如图所示:
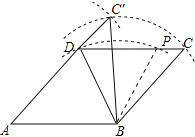
∵四边形ABCD是菱形,
∴AD=BC,∠A=∠BCD,
根据题意得:BC=B′C,BD=BP,DC′=PC,
∴AD=BC′,
在△BPC和△BDC′中,
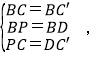
∴△BPC≌△BDC′(SSS),
∴∠BCD=∠C′,
∴∠A=∠C′;
(2)由(1)可知四边形ABC′D中,AB=AD=BC′,∠A=∠C,但四边形ABC′D不存在,易证A、D、C′共线,
所以有三条边相等且有一组对顶角相等的四边形是菱形”是真命题.
故答案为:真.

 名校课堂系列答案
名校课堂系列答案【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=![]() ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【题目】阳光市场某个体商户购进某种电子产品,每个进价是50元.调查发现,当售价是80元时,平均一周可卖出160个,而当售价每降低2元时,平均一周可多卖出20个.若设每个电子产品降价x元,
(1)根据题意,填表:
进价(元) | 售价(元) | 每件利润(元) | 销量(个) | 一周总利润(元) | |
降价前 | 50 | 80 | 30 | 160 |
|
降价后 | 50 |
(2)若商户计划每周盈利5200元,且尽量减少库存,则应降价多少元?