题目内容
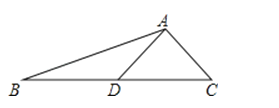
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=44°,∠BAD=28°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC= 度;
(2)求∠EDF的度数.

【答案】(1)100;(2)∠EDF=36°.
【解析】
(1)由折叠可得∠BAD=∠DAE=28°,即∠BAE=56°,根据三角形的外角等于不相邻的两个内角和,可求∠AFC的度数;
(2)根据三角形内角和定理可求∠ADB=108°,即可求∠ADF的度数,由折叠可求∠ADE=∠ADB=108°,即可求∠EDF的度数.
(1)∵折叠,∴∠BAD=∠DAE=28°,∴∠BAE=56°.
∵∠AFC=∠ABC+∠BAE,∴∠AFC=44°+56°=100°.
故答案为:100度.
(2)由折叠的性质可得:∠ADB=∠ADE.
∵∠ADF是△ABD的外角,∴∠ADF=∠B+∠BAD.
∵∠B=44°,∠BAD=28°.
又∵∠B+∠BAD+∠ADB=180°,∴∠ADF=44°+28°=72°,∠ADB=∠ADE=180°﹣44°﹣28°=108°.
∵∠ADE=∠EDF+∠ADF,∴∠EDF=∠ADE﹣∠ADF=108°﹣72°=36°.

练习册系列答案
相关题目