题目内容
【题目】如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )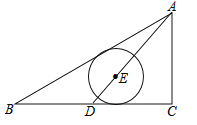
A.![]() ≤R≤
≤R≤![]()
B.![]() ≤R≤
≤R≤![]()
C.![]() ≤R≤2
≤R≤2
D.1≤R≤![]()
【答案】B
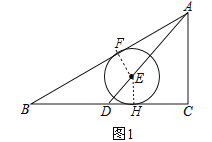
【解析】解:当点E在AD上,AD为△ABC的中线,如图1,作EH⊥BC于H,EF⊥AB于F,
∵以E为圆心的⊙E分别与AB、BC相切,
∴EH=EF=R,
在Rt△ABC中,∵∠C=90°,AB=5,AC=3,
∴BC=![]() =4,
=4,
∵点D为BC的中点,
∴BD=CD=2,
在Rt△ADC中,AD=![]() =
=![]() ,
,
∵EH∥AC,
∴△DEH∽△DAC,
∴![]() =
=![]() =
=![]() , 即
, 即![]() =
=![]() =
=![]() ,
,
∴DE=![]() R,DH=
R,DH=![]() R,
R,
∴AE=AD﹣DE=![]() ﹣
﹣![]() R,BH=BD+DH=2+
R,BH=BD+DH=2+![]() R,
R,
∵以E为圆心的⊙E分别与AB、BC相切,
∴BF=BH=2+![]() R
R
∴AF=AB﹣BF=3﹣![]() R,
R,
在Rt△AEF中,∵EF2+AF2=AE2 ,
∴R2+(3﹣![]() R)2=(
R)2=(![]() ﹣
﹣![]() R)2 , 解得R=
R)2 , 解得R=![]() ;
;
当点D运动到点C的位置,如图2,作EF⊥AB于F,
∵以E为圆心的⊙E分别与AB、BC相切,
∴EC=EF=R,
∴AE=AC﹣EC=3﹣R,
∵∠FAE=∠CAB,
∴Rt△AFE∽Rt△ACB,
∴![]() =
=![]() , 即
, 即![]() =
=![]() , 解得R=
, 解得R=![]() ,
,
∴当D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为![]() ≤R≤
≤R≤![]() .
.
故选B.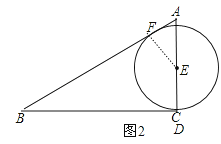
【考点精析】掌握切线的性质定理是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目