题目内容
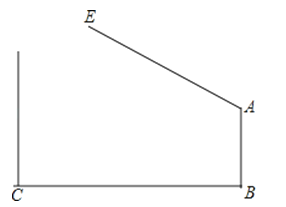
【题目】如图,AD是△ABC的中线,tanB=![]() , cosC=
, cosC=![]() , AC=
, AC=![]() . 求:
. 求:
(1)BC的长;
(2)sin∠ADC的值.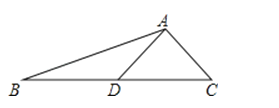
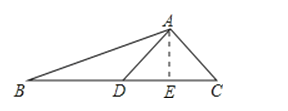
【答案】解:(1)过点A作AE⊥BC于点E,
∵cosC=![]() ,
,
∴∠C=45°,
在Rt△ACE中,CE=ACcosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=![]() ,即
,即![]() =
=![]() ,
,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)∵AD是△ABC的中线,
∴CD=![]() BC=2,
BC=2,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC=![]() .
.
【解析】(1)过点A作AE⊥BC于点E,根据cosC=![]() , 求出∠C=45°,求出AE=CE=1,根据tanB=
, 求出∠C=45°,求出AE=CE=1,根据tanB=![]() , 求出BE的长即可;
, 求出BE的长即可;
(2)根据AD是△ABC的中线,求出BD的长,得到DE的长,得到答案.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目
【题目】我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式组是否也具有类似的性质呢?请解答下列问题.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.