题目内容
【题目】如图，在平面直角坐标系中，O 为坐标原点，长方形 OABC，点 B 的坐标为（3，8），点 A、C 分别在坐标轴上，D 为 OC 的中点.
（1）在 x 轴上找一点 P，使得 PD＋PB 最小，则点 P 的坐标为 ；
（2）在 x 轴上找一点 Q，使得|QD－QB|最大，求出点 Q 的坐标并说明理由.
【答案】(1) P（1，0）;(2)见解析.
【解析】
（1）作点D关于x轴的对称点D'，根据轴对称性质有PD=PD'，又根据三角形两边之和PD'+PB大于第三边BD'，故B、P、D'在同一直线上时，PD+PB有最小值．求直线BD'的解析式后令y=0，求出其与x轴的交点，即此时的点P坐标;
（2）根据三角形两边之差|QD-QB|小于第三边BD，故当B、D、Q在同一直线上时，|QD-QB|=BD有最大值．求直线BD解析式后令y=0，求出此时Q的坐标．
解：（1）作D关于x轴的对称点D'，连接BD'，交x轴于点P
∵PD=PD'
∴PD+PB=PD'+PB
∴当B、P、D'在同一直线上时，PD+PB=BD'最小
∵四边形OABC是矩形，B（3，8）
∴C（0，8）
∵D为OC中点
∴D（0，4）
∴D'（0，-4）
设直线BD'解析式为：y=kx+b
， 解得：
，
∴直线BD'：y=4x-4
当4x-4=0时，解得：x=1
故答案为：P（1，0）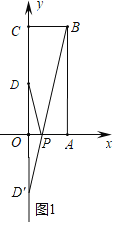
（2）根据三角形两边之差小于第三边，|QD-QB|＜BD
∴当B、D、Q在同一直线上时，|QD-QB|=BD最大
设直线BD解析式为：y=ax+c
， 解得：
∴直线BD：y=
x+4
当x+4=0时，解得：x=-3
∴点Q（-3，0）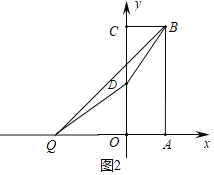
练习册系列答案
相关题目
