题目内容
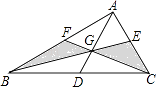
【题目】如图,在正方形ABCD中,点E,F分别在边AD,CD上,

(1)若AB=6,AE=CF,点E为AD的中点,连接AE,BF.
①如图1,求证:BE=BF=3![]() ;
;
②如图2,连接AC,分别交AE,BF于M,M,连接DM,DN,求四边形BMDN的面积.
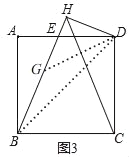
(2)如图3,过点D作DH⊥BE,垂足为H,连接CH,若∠DCH=22.5°,则![]() 的值为 (直接写出结果).
的值为 (直接写出结果).
【答案】(1)①详见解析;②12;(2)![]() .
.
【解析】
(1)①先求出AE=3,进而求出BE,再判断出△BAE≌△BCF,即可得出结论;
②先求出BD=6![]() ,再判断出△AEM∽△CMB,进而求出AM=2
,再判断出△AEM∽△CMB,进而求出AM=2![]() ,再判断出四边形BMDN是菱形,即可得出结论;
,再判断出四边形BMDN是菱形,即可得出结论;
(2)先判断出∠DBH=22.5°,再构造等腰直角三角形,设出DH,进而得出HG,BG,即可得出BH,结论得证.
解:(1)①∵四边形ABCD是正方形,
∴AB=BC=AD=6,∠BAD=∠BCD=90°,
∵点E是中点,
∴AE=![]() AD=3,
AD=3,
在Rt△ABE中,根据勾股定理得,BE=![]() =3
=3![]() ,
,
在△BAE和△BCF中,
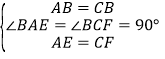
∴△BAE≌△BCF(SAS),
∴BE=BF,
∴BE=BF=3![]() ;
;
②如图2,连接BD,
在Rt△ABC中,AC=![]() AB=6
AB=6![]() ,
,
∴BD=6![]() ,
,
∵四边形ABCD是正方形,
∴AD∥BC,
∴△AEM∽△CMB,
∴![]() ,
,
∴![]() ,
,
∴AM=![]() AC=2
AC=2![]() ,
,
同理:CN=2![]() ,
,
∴MN=AC﹣AM﹣CN=2![]() ,
,
由①知,△ABE≌△CBF,
∴∠ABE=∠CBF,
∵AB=BC,∠BAM=∠BCN=45°,
∴△ABM≌△CBN,
∴BM=BN,
∵AC是正方形ABCD的对角线,
∴AB=AD,∠BAM=∠DAM=45°,
∵AM=AM,
∴△BAM≌△DAM,
∴BM=DM,
同理:BN=DN,
∴BM=DM=DN=BN,
∴四边形BMDN是菱形,
∴S四边形BMDN=![]() BD×MN=
BD×MN=![]() ×6
×6![]() ×2
×2![]() =12;
=12;
(2)如图3,设DH=a,
连接BD,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∵DH⊥BH,
∴∠BHD=90°,
∴点B,C,D,H四点共圆,
∴∠DBH=∠DCH=22.5°,
在BH上取一点G,使BG=DG,
∴∠DGH=2∠DBH=45°,
∴∠HDG=45°=∠HGD,
∴HG=HD=a,
在Rt△DHG中,DG=![]() HD=
HD=![]() a,
a,
∴BG=![]() a,
a,
∴BH=BG+HG=![]() A+A=(
A+A=(![]() +1)a,
+1)a,
∴![]() .
.
故答案为:![]() .
.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案