题目内容
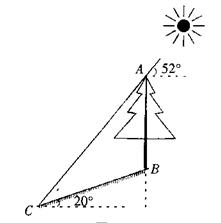
如图,在一个坡角为20º的斜坡上方有一棵树,高为AB,当太阳光线与水平线成52º角时,测得该树在斜坡上的树影BC的长为10m,求树高AB(精确到0.1m).
(已知:sin20º≈0.342,cos20º≈0.940,tan20º≈0.364,sin52º≈0.788,cos52º≈0.616,tan52º≈1.280)
(已知:sin20º≈0.342,cos20º≈0.940,tan20º≈0.364,sin52º≈0.788,cos52º≈0.616,tan52º≈1.280)

过点C作CD⊥AB,交AB的延长线于点D.
在Rt△BCD中,∠BCD=20°,BC=10,
则BD=BC·sin20°≈10×0.342=3.42,
CD=BC·cos20°≈10×0.940=9.4.
在Rt△ACD中,∠ACD=52°,
则AD=CD·tan52º≈9.4×1.280≈12.03,
所以AB=AD-BD≈12.03-3.42≈8.6(m).
答:树高AB约8.6m.
在Rt△BCD中,∠BCD=20°,BC=10,
则BD=BC·sin20°≈10×0.342=3.42,
CD=BC·cos20°≈10×0.940=9.4.
在Rt△ACD中,∠ACD=52°,
则AD=CD·tan52º≈9.4×1.280≈12.03,
所以AB=AD-BD≈12.03-3.42≈8.6(m).
答:树高AB约8.6m.
略

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
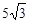 ,那么∠A= ▲ 度.
,那么∠A= ▲ 度.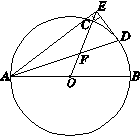
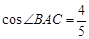 ,求
,求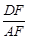 的值.
的值.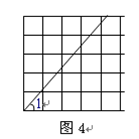

 ,sin54°="0.81 " cos54°=0.59,tan54°=1.38,sin70°=0.94,cos70°=0.34,tan70°=2.75)
,sin54°="0.81 " cos54°=0.59,tan54°=1.38,sin70°=0.94,cos70°=0.34,tan70°=2.75)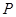 ,军舰
,军舰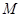 停泊在雷达站
停泊在雷达站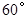 方向36海里处,另一艘军舰
方向36海里处,另一艘军舰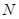 位于军舰
位于军舰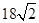 海里.求:
海里.求:
 的距离.(结果保留根号)
的距离.(结果保留根号)