题目内容
【题目】如图在△ABC中，∠ACB＝60°，D是AB边的中点，E是边BC上一点，若DE平分△ABC的周长，且DE＝
，则AC的长为_____．
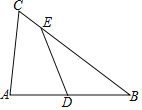
【答案】2．
【解析】
延长BC至M，使CM=CA，连接AM，作CN⊥AM于N，根据题意得到ME=EB，根据三角形中位线定理得到DE=
AM，根据等腰三角形的性质求出∠ACN，根据正弦的概念求出AN，计算即可．
延长BC至M，使CM=CA，连接AM，作CN⊥AM于N，如图所示：
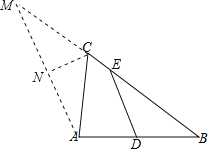
设AC=x，
DE平分△ABC的周长，
∴ME=EB，
又∵AD=DB，
∴DE=AM，DE∥AM，
∵∠ACB=60°，
∴∠ACM=120°，
∵CM=CA，
∴∠ACN=60°，AN=MN，
∴AN=ACsin∠ACN=
x，
∴AM=2DE=2AN=2
，
∴AC=2，
故答案为：2．
练习册系列答案
相关题目
