Question

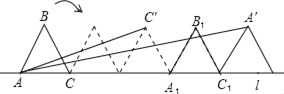
【题目】如图，已知边长为2的正三角形ABC沿着直线l滚动．

(1)当△ABC滚动一周到△A1B1C1的位置，此时A点运动的路程为　 　；约为　　；(精确到0.1，π＝3.14…)

(2)设△ABC滚动240°时，C点的位置为C′，△ABC滚动480°时，A点的位置为A′．请你利用三角函数中正切的两角和公式tan(α+β)＝(tanα+tanβ)÷(1﹣tanαtanβ)，求出∠CAC′+∠CAA′的度数．

Answer 1

【答案】(1)8.37758；8.4；(2)∠CAC′+∠CAA′＝30°．

【解析】

（1）由图形可以看出，△ABC滚动的轨迹正好为两个半径为2的三分之一的圆周长；
（2）先求出正三角形的高，再利用三角函数求出tan∠CAC’与tan∠CAA′的值，然后通过等量代换求出∠CAC′＋∠CAA′的度数．

(1)当△ABC滚动一周到△A1B1C1的位置，此时A点运动的路径为两个半径为2的三分之一的圆周长，

即A点的路程长为：2××2×3.14×2＝8.37758；

约为8.4．

(2)设△ABC滚动240°时，C点的位置为C’，△ABC滚动480°时，A点的位置为A′．

∵正△ABC的边长为2

∴正△ABC的高为

tan∠CAC′＝

tan∠CAA′＝＝

所以：由公式tan(α＋β)＝(tanα＋tanβ)÷(1﹣tanαtanβ)，

得：tan(∠CAC′＋∠CAA′)

＝(tan∠CAC′＋tan∠CAA′)÷(1﹣tan∠CAC′tan∠CAA′)

＝(＋)÷(1﹣×)

＝．

所以：∠CAC′＋∠CAA′＝30°．