题目内容
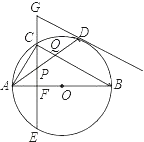
【题目】如图的矩形ABCD中,E为AB的中点,有一圆过C、D、E三点,且此圆分别与AD、BC相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下:
(甲) 作∠DEC的角平分线L,作DE的中垂线,交L于O点,则O即为所求;
(乙) 连接PC、QD,两线段交于一点O,则O即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )
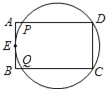
A. 两人皆正确 B. 两人皆错误
C. 甲正确,乙错误 D. 甲错误,乙正确
【答案】A
【解析】
根据线段垂直平分线的性质判断甲,根据90°的圆周角所对的弦是直径判断乙.
解:甲,∵ED=EC,
∴△DEC为等腰三角形,
∴L为CD之中垂线,
∴O为两中垂线之交点,
即O为△CDE的外心,
∴O为此圆圆心.
乙,∵∠ADC=90°,∠DCB=90°,
∴PC、QD为此圆直径,
∴PC与QD的交点O为此圆圆心,因此甲、乙两人皆正确.
故选:A.

练习册系列答案
相关题目