题目内容
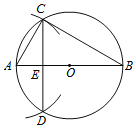
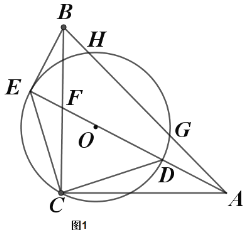
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 的延长线相交于点
的延长线相交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]()
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
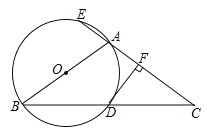
【答案】(1)见解析;(2)![]() .
.
【解析】
((1)由等腰三角形的性质可证∠ODB=∠C,从而OD//AC,可证OD⊥DF,即可解决问题;
(2)连结BE,根据直径所对的圆周角为直角得出![]() ,根据已知用AE表示出AB、EC、BE,从而可得
,根据已知用AE表示出AB、EC、BE,从而可得![]() ,然后由△DFC∽△BEC,得
,然后由△DFC∽△BEC,得![]() ,由此即可计算CF长.
,由此即可计算CF长.
(1)证明:如图,连接OD,
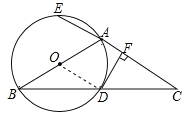
∵OB=OD,∴∠B=∠ODB.
∵AB=AC,∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线
(2)解:如图,连接BE,
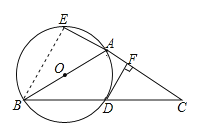
∵AB是直径,
∴∠AEB=90°.
∵AB=AC,AC=3AE,
∴AB=3AE,CE=4AE,
∴BE=![]() =
=![]() AE,
AE,
∴![]() .
.
∵∠DFC=∠AEB=90°,
∴DF∥BE,
∴△DFC∽△BEC,
∴![]() ,
,
∴DF=![]() FC.
FC.
∵DF=2,
∴CF=![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目