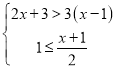题目内容
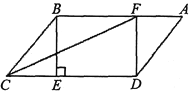
【题目】在□ABCD中,BE⊥CD于点E,点F在AB上,且AF=CE,连接DF.
(1)求证:四边形BEDF是矩形;
(2)连接CF,若CF平分∠BCD,且CE=3,BE=4,求矩形BEDF的面积.
【答案】(1)证明见解析;(2)S矩形BEDF=20.
【解析】
(1)根据有一个角是直角的平行四边形是矩形证明即可;
(2)利用等腰三角形的性质求出BF即可解决问题.
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,
∵AF=CE,
∴AB-AF=CD-CE,即BF=DE,
∴四边形BEDF是平行四边形,
又∵BE⊥CD,
∴∠BED=90°,
∴![]() BEDF是矩形.
BEDF是矩形.
(2)∵CF平分∠BCD,
∴∠BCF=∠DCF,
∵AB//CD,
∴∠BFC=∠DCF,
∴∠BCF=∠BFC,
∴BC=BF.
在Rt△BCE中,BC=![]() =5.
=5.
∴BC=BF=5,
∴S矩形BEDF=BF![]() BE=5×4=20.
BE=5×4=20.

练习册系列答案
相关题目