题目内容
【题目】一张桌子可坐6人,按下列方式将桌子拼在一起.

①2张桌子拼在一起可坐_____人,4张桌子拼在一起可坐_______人,![]() 张桌子拼在一起可坐(_____________)人.
张桌子拼在一起可坐(_____________)人.
②一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐__________人.
③若在②中,改成8张桌子拼成一张大桌子,则共可坐________人.
【答案】(1)8,12,2n+4;(2)112人;(3)100
【解析】
根据图形查出2张桌子,3张桌子可坐的人数,然后得出每多一张桌子可多坐2人的规律,然后解答;
②求出每一张大桌子可坐的人数与可拼成的大桌子数,然后相乘计算即可;
③求出每一张大桌子可坐的人数与可拼成的大桌子数,然后相乘计算即可.
①2张:6+2=8,
3张:8+2=10,
4张:10+2=12,
第n张:6+2(n-1)=2n+4;
②当n=5时,2n+4=2×5+4=14人,
可拼成的大桌子数,40÷5=8,
14×8=112人;
③当n=8时,2n+4=2×8+4=20人,
可拼成的大桌子数,40÷8=5,
20×5=100人
故答案为:①8,12,2n+4,②112,③100.

练习册系列答案
相关题目
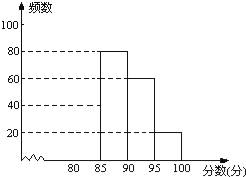
【题目】某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
分数段 | 频数 | 频率 |
80≤x<85 | x | 0.2 |
85≤x<90 | 80 | y |
90≤x<95 | 60 | 0.3 |
95≤x<100 | 20 | 0.1 |
根据以上图表提供的信息,解答下列问题:
(1)写出表中x,y的数值;
(2)请补全频数分布直方图;
(3)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(4)获奖成绩的中位数落在哪个分数段?