Question

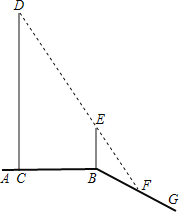
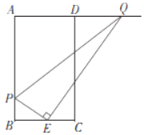
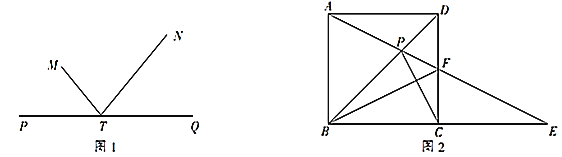
【题目】如图1，直线PQ的同侧有两点M，N，点T在直线PQ上，若∠MTP=∠NTQ，则称点M，N为关于直线PQ的衍射点．如图2，BD是矩形ABCD的对角线，E是边BC延长线上的一点，且CE=BC，连接AE交CD于点F，交BD于点P，连接BF，CP．

(1)求证：点A，B是关于直线CD的衍射点．

(2)若点C，F是关于直线BD的衍射点，CP=2PF=2，求AB的长．

Answer 1

【答案】（1）见解析（2）6

【解析】

（1）由矩形的性质得∠BCD=90°,因为BC=CE,可得FB=FE,故可得∠BFC=∠EFC,，再由∠AFD=∠EFC可得∠AFD=∠BFC进而得到结论；

（2）首先证明△ADF≌△ECF得出F点是DC的中点，再证明△DPF∽△BPA求得，进而得出AP=CP，再证明△ABP≌△CBP得出AB=BC, 作PQ⊥AB，垂足为点Q，运用勾股定理求出AQ的长以及BQ的长，从而可得AB的长.

∵四边形ABCD是矩形，

∴∠BCD=90°，

∵BC=CE,

∴FC垂直平分BE，

∴BF=EF，

∴∠BFC=∠EFC,

∵∠AFD=∠EFC,

∴∠AFD=∠BFC,

∴点A，B是关于直线CD的衍射点;

（2）∵BC=CE,

又∵BC=AD，

∴CE=AD

在△ADF和△ECF中，

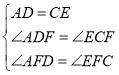
∴△ADF≌△ECF,

∴DF=CF=,

∵DF∥AB,

∴△DPF∽△BPA

∴,即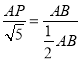

∴,

∵,

∴AP=CP,

又∵点C，F是关于直线BD的衍射点，

∴∠BPC=∠DPF,

∵∠DPF=∠APB,

∴∠BPC=∠APB,

∵AP=PC,BP=BP,

∴△ABP≌△CBP,

∴∠ABP=∠CBP,AB=BC,

又∵四边形ABCD是矩形，

∴∠ABC=90°,

∴∠ABP=,

作PQ⊥AB，垂足为点Q，

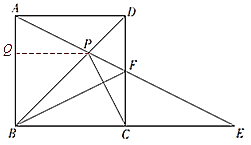
在Rt△BPQ中，BQ=PQ,

设BQ=x，∴PQ=x，

∵,

∴,即,

∴AQ=x，

在Rt△APQ中，,

∴

解得，

∴BQ=4,AQ=2,

∴AB=BQ+AB=4+2=6.