题目内容
【题目】如图,在矩形ABCD中,AB=4,BC=2,点E是边BC的中点,P为AB上一点,连接PE,过点E作PE的垂线交射线AD于点Q,连接PQ,设AP的长为t.
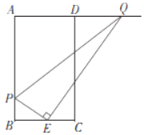
(1)用含t的代数式表示AQ的长;
(2)若△PEQ的面积等于10,求t的值.
【答案】(1)AQ=17-4t;(2)t的值为2.
【解析】
(1)通过勾股定理构建方程,即可得解;
(2)利用面积列出等式,构建方程,即可得解.
(1)延长BC,作QH⊥BC于H,如图所示:

∵AB=4,BC=2,点E是边BC的中点,AP的长为t
∴BP=AB-AP=4-t,BE=CE=1,
∵QH⊥BC
∴QH=AB=4,EH=BH-BE=AQ-BE=AQ-1
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]() ;
;
(2)由题意,得![]()
∴![]()
由(1)中,得
![]()
解得![]() 或
或![]()
∵AB=4,AP<AB
∴![]() .
.

练习册系列答案
相关题目