Question

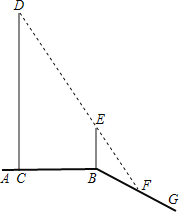
【题目】如图，平台AB上有一棵直立的大树CD，平台的边缘B处有一棵直立的小树BE，平台边缘B外有一个向下的斜坡BG．小明想利用数学课上学习的知识测量大树CD的高度．一天，他发现大树的影子一部分落在平台CB上，一部分落在斜坡上，而且大树的顶端D与小树顶端E的影子恰好重合，且都落在斜坡上的F处，经测量，CB长5米，BF长2米，小树BE高1.8米，斜坡BG与平台AB所成的∠ABG＝150°．请你帮小明求出大树CD的高度．

Answer 1

【答案】大树CD的高度为15.8米．

【解析】

延长CB交EF于点H，过点F作FM⊥EB的延长线于点M，在直角三角形MBF中，利用30°角的性质求出BM和MF，再利用相似求出BH长度；最后由△HBE∽△HCD，求出CD即大树的高度即可．

解：延长CB交EF于点H，过点F作FM⊥EB的延长线于点M，

∵∠ABG＝150°，BE⊥CB，

∴∠MBF＝150°﹣90°＝60°，

∴∠MFB＝30°，

∵BF的长为2米，

∴BM＝1米，MF＝米.

∵BE⊥CB，MF⊥BE，

∴BH∥MF，

∴△EBH∽△EMF，

∴＝.

又∵EB＝1.8米，

∴＝，

∴BH＝.

∵BE∥CD，

∴△HBE∽△HCD，

∴＝.

∵CB＝5，

∴＝，

∴CD＝15.8米.

∴大树CD的高度为15.8米．