题目内容
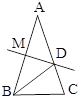
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,且AG=AB、CG的延长线交BA的延长线于点F,连接FD.试探究当∠BCD= °时,四边形ACDF是矩形,证明你的结论.
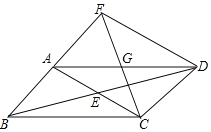
【答案】当∠BCD=120°时,四边形ACDF是矩形,证明见解析.
【解析】
根据平行四边形的性质证△AGF≌△DGC,根据全等三角形的性质可证AB=AF,四边形ACDF是平行四边形,进而证得AD=CF,根据对角线相等的平行四边形是矩形判断即可.
当∠BCD=120°时,四边形ACDF是矩形,
理由:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠AFC=∠DCG,
∵点G为AD的中点,
∴GA=GD,
又∠AGF=∠CGD,
∴△AGF≌△DGC(ASA),
∴AF=CD,
又AB∥CD,AB=CD,
∴AB=AF,四边形ACDF是平行四边形,
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD=120°,
∴∠FAG=60°,
∵AB=AG=AF,
∴△AFG是等边三角形,
∴AG=GF,
∵△AGF≌△DGC,
∴FG=CG,
∵AG=GD,
∴AD=CF,
∴四边形ACDF是矩形.
故答案为:120.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目