题目内容
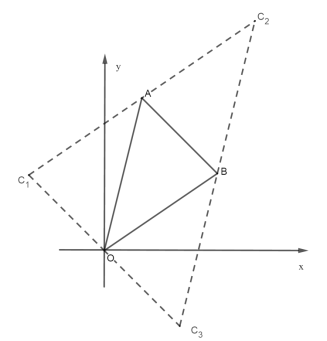
【题目】如图,在平面直角坐标系中,点A(1,4),点B(3,2),连接OA,OB.
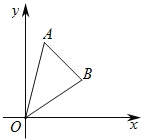
(1)求直线OB与AB的解析式;
(2)求△AOB的面积.
(3)下面两道小题,任选一道作答.作答时,请注明题号,若多做,则按首做题计入总分.
①在y轴上是否存在一点P,使△PAB周长最小.若存在,请直接写出点P坐标;若不存在,请说明理由.
②在平面内是否存在一点C,使以A,O,C,B为顶点的四边形是平行四边形.若存在,请直接写出点C坐标;若不存在,请说明理由.
【答案】(1)直线OB的解析式为![]() ,直线AB的解析式为y= -x+5(2)5;(3)①存在,(0,
,直线AB的解析式为y= -x+5(2)5;(3)①存在,(0,![]() );②存在,(2,-2)或(4,6)或(-2,2)
);②存在,(2,-2)或(4,6)或(-2,2)
【解析】
(1)根据题意分别设出两直线的解析式,代入直线上两点坐标即可求出直线OB与AB的解析式;
(2)延长线段AB交x轴于点D,求出D的坐标,分别求出![]() 、
、![]() 由
由![]() 即可求得;
即可求得;
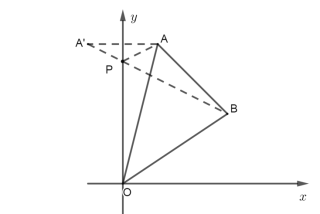
(3)①根据两点之间线段最短,A、B在y轴同侧,作出点A关于y的对称点![]() ,连接
,连接![]() B与y轴的交点即为所求点P;
B与y轴的交点即为所求点P;
②使以A,O,C,B为顶点的四边形是平行四边形,则分三种情况分析,分别以OA、AB、OB为对角线作出平行四边形,利用中点坐标公式代入求解即可.
解:(1)设直线OB的解析式为y=mx,
∵点B(3,2),
∴![]() ,
,
∴直线OB的解析式为![]() ,
,
设直线AB的解析式为y=kx+b,
根据题意可得:![]()
解之得![]()
∴直线AB的解析式为y= -x+5.
故答案为:直线OB的解析式为![]() ,直线AB的解析式为y= -x+5;
,直线AB的解析式为y= -x+5;
(2)如图,延长线段AB交x轴于点D,
当y=0时,-x+5=0,x=5,
∴点D横坐标为5,OD=5,
∴![]() ,
,
![]()
∴![]() ,
,
故答案为:5.
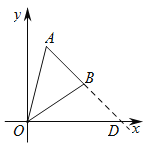
(3)①存在,(0,![]() );
);
过点A作y轴的对称点![]() ,连接
,连接![]() B,交y轴与点P,则点P即为使△PAB周长最小的点,
B,交y轴与点P,则点P即为使△PAB周长最小的点,
由作图可知,点![]() 坐标为
坐标为![]() ,又点B(3,2)
,又点B(3,2)
则直线![]() B的解析式为:
B的解析式为:![]() ,
,
∴点P坐标为![]() ,
,
故答案为:![]() ;
;
②存在. ![]() 或
或![]() 或
或![]() .
.
有三种情况,如图所示:设点C坐标为![]() ,
,
当平行四边形以AO为对角线时,
由中点坐标公式可知,AO的中点坐标和BC中点坐标相同,
∴![]()
解得![]()
∴点![]() 坐标为
坐标为![]() ,
,
当平行四边形以AB为对角线时,AB的中点坐标和OC的中点坐标相同,则
![]()
![]()
∴点![]() 的坐标为
的坐标为![]() ,
,
当平行四边形以BO为对角线时,BO的中点坐标和AC的中点坐标相同,则
![]()
解得![]()
∴点![]() 坐标为
坐标为![]() ,
,
故答案为:存在,![]() 或
或![]() 或
或![]() .
.