Question

【题目】如图，点A(m，m+1)，B(m+3，m1)都在反比例函数的图象上，如果M为x轴上一点，N为y轴上一点，以点A，B，M，N为顶点的四边形是平行四边形，直接写出点M，N的坐标：____________.

Answer 1

【答案】

【解析】

根据反比例函数解析式求得k=xy；然后利用反比例函数图象上点的坐标特征列出关于m的方程k=m（m+1）=（m+3）（m-1），从而求得k、m的值，得出A,B的坐标，在分情况讨论，这样的平行四边形有2个：点M分别位于x轴的正负半轴上、点N分别位于y轴的正负半轴上．

∵点A(m,m+1),B(m+3,m1)都在反比例函数y=kx的图象上，

∴,

∴k=m(m+1)=(m+3)(m1)，

∴m2+m=m2+2m3，

解得m=3，

∴k=3×4=12；

∵m=3，

∴A(3,4),B(6,2)，

作AM⊥x轴于M，过B作BN⊥y轴于N，两线交于P，

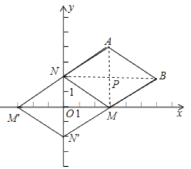
∵A(3,4),B(6,2)，

∴AP=PM=2，BP=PN=3，

∵四边形ANMB是平行四边形，

当M(3,0)、N(0,2)时，根据勾股定理能求出AM=BN，AB=MN，

即四边形AMNB是平行四边形，

∴此时M(3,0)、N(0,2)或M(3,0)、N(0,2).