题目内容
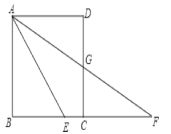
【题目】如图，点E是正方形ABCD的边BC上的一点，∠DAE的平分线AF交BC的延长线于点F，交CD于点G，若AB=8，BF=16，求CE的长；.
【答案】2
【解析】
求出AE=EF，设CE=x，则BC=8-x，EF=AE=8+x，在Rt△ABE中，由勾股定理得出方程82+（8-x）2=（8+x）2，求出方程的解即可；
∵四边形ABCD是正方形，
∴AB=BC=8,∠B=90°,AD∥BC，
∴∠DAG=∠F，
∵AF平分∠DAE，
∴∠DAG=∠EAF，
∴∠EAF=∠F，
∴AE=EF，
设CE=x，则BC=8x，EF=AE=16-（8-x）=8+x，
在Rt△ABE中,由勾股定理得：82+(8x)2=(8+x)2，
x=2，
即CE=2；
练习册系列答案
相关题目
【题目】如图，△ABC、△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝
．将△BDE绕点B逆时针方向旋转后得△BD'E'，当点E'恰好落在线段AD'上时，则CE'＝_______．
【题目】某快餐店共有10名员工，所有员工工资的情况如下表：
人员 | 店长 | 厨师甲 | 厨师乙 | 会计 | 服务员甲 | 服务员乙 | 勤杂工 |
人数 | 1 | 1 | 1 | 1 | 1 | 3 | 2 |
工资额 | 20000 | 7000 | 4000 | 2500 | 2200 | 1800 | 1200 |
请解答下列问题：
（1）餐厅所有员工的平均工资是 ；所有员工工资的中位数是 ．
（2）用平均数还是用中位数描述该餐厅员工工资的一般水平比较恰当？
（3）去掉店长和厨师甲的工资后，其他员工的平均工资是多少？它是否也能反映该快餐店员工工资的一般水平？
