题目内容
【题目】如图,在长方形ABCD中,AB=5,AD=12,点E是BC上一点,将△ABE沿AE折叠,使点B落在点F处,连接CF,当△CEF为直角三角形时,CF的长为________。

【答案】8或![]()
【解析】
分情况讨论,当∠FEC为直角时,由折叠图形的特点推得四边形ABEF为正方形,从而求得EF和EC的长,利用勾股定理可求FC的长;当∠EFC为直角时,推得A、F、C在一条直线上,由勾股定理求得AC,再由折叠图形的特点求出AF的长,则FC的长度可知.
如图,①当∠FEC为直角时,
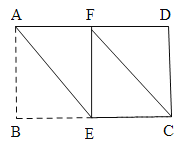
∵∠BEF=90°,
∵EB=EF,
∴四边形ABEF为正方形,
∴BE=AB=EF=5,
∴EC=BC-BE=12-5=7,
∴FC=![]()
②如图,当∠EFC为直角时
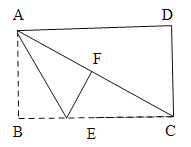
∵∠AFC=∠ABE=90°,
∴A、F、C在同一条直线上,
AC=![]()
∵AF=AB=5,
∴CF=AC-AF=13-5=8.
故答案为:8或![]()

练习册系列答案
相关题目