Question

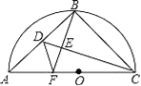
【题目】如图，已知以AB为直径的圆中，∠ACB＝∠ABD＝90°，∠D＝60°，∠ABC＝45°.

(1)求证：EC平分∠AEB；

(2)求的值．

Answer 1

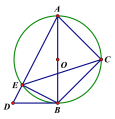
【答案】(1)见详解；(2).

【解析】

由Rt△ACB中∠ABC=45°，得出∠BAC=∠ABC=45°，根据圆周角定理得出∠AEC=∠ABC，∠BEC=∠BAC，等量代换得出∠AEC=∠BEC，即EC平分∠AEB；
（2）方法1、设AB与CE交于点M．根据角平分线的性质得出=．易求∠BAD=30°，由直径所对的圆周角是直角得出∠AEB=90°，解直角△ABE得到AE= BE，那么== ．作AF⊥CE于F，BG⊥CE于G．证明△AFM∽△BGM，根据相似三角形对应边成比例得出 = =，进而求出 = == ．
方法2、易求∠BAD=30°，由直径所对的圆周角是直角得出∠AEB=90°，解直角△ABE得到AE= BE，那么 == ，再用角平分线定理判断出CP=CQ，即可得出结论．

（1）证明：∵Rt△ACB中，∠ACB=90°，∠ABC=45°，
∴∠BAC=∠ABC=45°，
∵∠AEC=∠ABC，∠BEC=∠BAC，
∴∠AEC=∠BEC，
即EC平分∠AEB；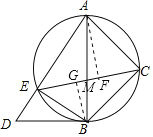

（2）解：如图，设AB与CE交于点M．
∵EC平分∠AEB，
∴ =．
在Rt△ABD中，∠ABD=90°，∠D=60°，
∴∠BAD=30°，
∵以AB为直径的圆经过点E，
∴∠AEB=90°，
∴tan∠BAE= =，
∴AE=BE，
∴ == ．
作AF⊥CE于F，BG⊥CE于G．
在△AFM与△BGM中，
∵∠AFM=∠BGM=90°，∠AMF=∠BMG，
∴△AFM∽△BGM，
∴ = = ，
∴ = ==．

方法2、如图1，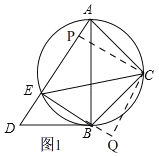
在Rt△ABD中，∠ABD=90°，∠D=60°，
∴∠BAD=30°，
∵以AB为直径的圆经过点E，
∴∠AEB=90°，
∴tan∠BAE= =，
∴ AE= BE，
过点C作CP⊥AE于P，过点C作CQ⊥EB交延长线于Q，
由（1）知，EC是∠AEB的角平分线，
∴CP=CQ，
∴ = = =