题目内容
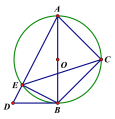
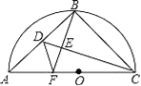
【题目】如图,半圆O的直径AC=2![]() ,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为_____.
,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为_____.
【答案】![]()
【解析】
分两种情形讨论:①当∠DFE=∠BCE时,可以证明DB=DC,BC=CF,∠DFC=∠DBC=90°即可解决问题.②当∠FDE=∠BCE时,可以证明DF∥BC、△BDF∽△CBD得到![]() =
=![]() 列出方程解决问题.
列出方程解决问题.
解: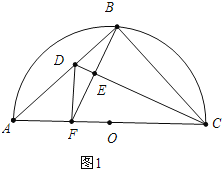
①如图1,当∠DFE=∠BCE时,
∵∠DEF=∠BEC,
∴△DEF∽△BEC,
∵AC是直径,
∴∠ABC=90°,
∵BF⊥CD,
∴∠CEB=90°,
∴∠BCE+∠CBE=90°,∠DBE+∠EBC=90°,
∴∠DBE=∠BCE=∠DFE,
∴DB=DF,
∵DE⊥BF,
∴EB=EF,
∴BC=CF,
∵点B为半圆的中点,
∴AB=BC,
∴∠A=45°,
∵∠DBF=∠DFB,∠CBF=∠CFB,∠DBF+∠CBF=90°,
∴∠DFB+∠CFB=90°,
∴∠DFC=∠DFA=90°,
∴∠A=∠ADF=45°,
∴AF=DF=BD,
在RT△ABC中,∵AC=2![]() ,
,
∴AB=BC=![]() AC=2,
AC=2,
∴FC=2,
∴BD=AF=AC-FC=2![]() -2,
-2,
②如图2,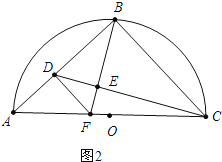
当∠FDE=∠BCE时,
∵∠DEF=∠BEC,
∴△DEF∽△CEB,DF∥BC,
∴∠ADF=∠ABC=90°,
∵∠ABC=∠BEC=90°,
∴∠BCE+∠CBE=90°,∠DBE+∠EBC=90°,
∴∠DBE=∠BCE=∠FDE,
∵∠BDF=∠DBC=90°,∠DBF=∠BCD,
∴△BDF∽△CBD,
∴![]() =
=![]() ,
,
∵∠A=45°,∠ADF=90°,
∴∠AFD=∠A=45°,
∴AD=DF,
设BD=x,由(1)可知:AB=BC=2,AD=DF=2-x,
∴![]() =
=![]() ,整理得:x2+2x-4=0,
,整理得:x2+2x-4=0,
解得:x= -1+![]() (或-1-
(或-1-![]() 舍弃)
舍弃)
∴BD=![]() -1.
-1.
故答案为2![]() -2或
-2或![]() -1.
-1.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案