题目内容
【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ. 
(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP= ![]() ,求NQ的长.
,求NQ的长.
【答案】
(1)证明:连结OP,如图,
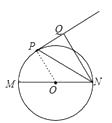
∴直线PQ与⊙O相切,
∴OP⊥PQ,
∵OP=ON,
∴∠ONP=∠OPN,
∵NP平分∠MNQ,
∴∠ONP=∠QNP,
∴∠OPN=∠QNP,
∴OP∥NQ,
∴NQ⊥PQ
(2)解:连结PM,如图,
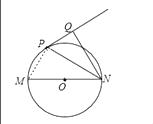
∵MN是⊙O的直径,
∴∠MPN=90°,
∵NQ⊥PQ,
∴∠PQN=90°,
而∠MNP=∠QNP,
∴Rt△NMP∽Rt△NPQ,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴NQ=3.
【解析】(1)连结OP,根据切线的性质由直线PQ与⊙O相切得OP⊥PQ,再由OP=ON得到∠ONP=∠OPN,由NP平分∠MNQ得到∠ONP=∠QNP,利用等量代换得∠OPN=∠QNP,根据平行线的判定得OP∥NQ,所以NQ⊥PQ;(2)连结PM,根据圆周角定理由MN是⊙O的直径得到∠MPN=90°,易证得Rt△NMP∽Rt△NPQ,然后利用相似比可计算出NQ的长.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
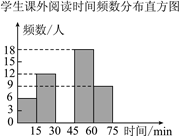
【题目】某校要了解学生每天的课外阅读时间情况,随机调查了部分学生,对学生每天的课外阅读时间x(单位:min)进行分组整理,并绘制了如图所示的不完整的统计图表,根据图中提供的信息,解答下列问题:
(1)本次调查共抽取了________名学生;
(2)统计表中a=________,b=________;
(3)将频数分布直方图补充完整;
(4)若全校共有1200名学生,请估计阅读时间不少于45 min的有多少人.
课外阅读时间x/min | 频数/人 | 百分比 |
0≤x<15 | 6 | 10% |
15≤x<30 | 12 | 20% |
30≤x<45 | a | 25% |
45≤x<60 | 18 | b |
60≤x<75 | 9 | 15% |