题目内容
【题目】抛物线C:y=![]() x[a(x﹣1)+x+1](a为任意实数).
x[a(x﹣1)+x+1](a为任意实数).
(1)无论a取何值,抛物线C恒过定点 , .
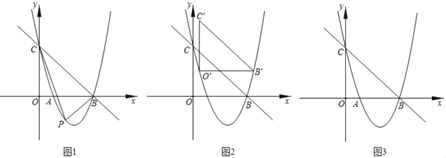
(2)当a=1时,设抛物线C在第一象限依次经过的整数点(横、纵坐标均为整数的点)为A1,A2,……An,将抛物线C沿着直线y=x(x≥0)平移,将平移后的抛物线记为C n,抛物线C n经过点An,C n的顶点坐标为Mn(n为正整数且n=1,2,…,n,例如n=1时,抛物线C1经过点A1,C1的顶点坐标为M1).
①抛物线C2的解析式为 ,顶点坐标为 .
②抛物线C1上是否存在点P,使得PM1∥A2M2?若存在,求出点P的坐标,并判断四边形PM1M2A2的形状;若不存在,请说明理由.
③直接写出Mn﹣1,Mn两顶点间的距离: .
【答案】(1)(0,0),(1,1);(2)①y=(x﹣3)2+3,(3,3).②存在,P(0,2),③2![]() .
.
【解析】
(1)分别取x=0,x=1求出对应的函数值即可解决问题;
(2)①由题意a=1,可得抛物线的解析式为y=x2,设平移后的顶点为(m,m),则平移后的抛物线为y=(x﹣m)2+m,利用待定系数法求出m即可;
②求出A1,M1,A2,M2的坐标,利用图象法解决问题即可;
③分别求出Mn,Mn﹣1的坐标,利用两点间距离公式求解即可.
解:(1)对于y=![]() x[a(x﹣1)+x+1],
x[a(x﹣1)+x+1],
当x=0时,y=0,
当x=1时,y=1,
∴抛物线C经过定点(0,0)和(1,1),
故答案为:(0,0),(1,1);
(2)①由题意a=1,可得抛物线的解析式为y=x2,
设平移后的顶点为(m,m),
则平移后的抛物线为y=(x﹣m)2+m,
∵抛物线C2经过A2(2,4),
∴4=(2﹣m)2+m,
解得m=3或0(舍弃),
∴抛物线C2的解析式为y=(x﹣3)2+3,顶点M2(3,3).
故答案为:y=(x﹣3)2+3,(3,3);
②存在.由题意A1(1,1),M1(1,1).A2(2,4),M2(3,3),
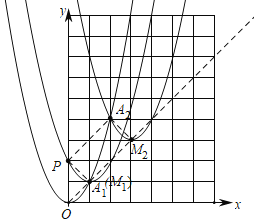
观察图象可知当P(0,2)时,PA1∥A2M2,此时四边形PM1M2A2是矩形;
③由题意An(n,n2),An﹣1[n﹣1,(n﹣1)2],
设抛物线Cn的解析式为y=(x﹣m)2+m,
∵Cn经过An,
∴n2=(n﹣m)2+m,
解得m=2n﹣1或0(舍弃),
∴Mn(2n﹣1,2n﹣1),
同法可得Mn﹣1(2n﹣3,2n﹣3),
∴MnMn﹣1=![]() =2
=2![]() ,
,
故答案为:2![]() .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案