题目内容
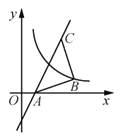
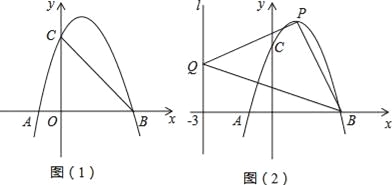
【题目】如图1,抛物线y=ax2﹣![]() x+c交x轴于A,B两点,交y轴于点C.直线y=﹣
x+c交x轴于A,B两点,交y轴于点C.直线y=﹣![]() x+3经过点B,C.
x+3经过点B,C.
(1)求抛物线的解析式;
(2)若点P为直线BC下方的抛物线上一动点(不与点B,C重合),则△PBC的面积能够等于△BOC的面积吗?若能,求出相应的点P的坐标;若不能,请说明理由;
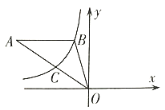
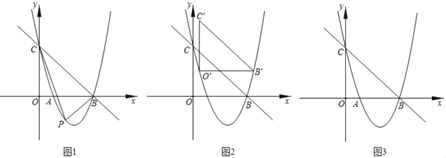
(3)如图2,现把△BOC平移至如图所示的位置,此时三角形水平方向一边的两个端点点O′与点B′都在抛物线上,称点O′和点B′为△BOC在抛物线上的一“卡点对”;如果把△BOC旋转一定角度,使得其余边位于水平方向然后平移,能够得到这个三角形在抛物线上新的“卡点对”.请直接写出△BOC在已知抛物线上所有“卡点对”的坐标.
【答案】(1)![]() ;(2)即当(2,﹣
;(2)即当(2,﹣![]() )时,两个三角形面积相同;(3)故抛物线上所有“卡点对”的坐标(
)时,两个三角形面积相同;(3)故抛物线上所有“卡点对”的坐标(![]() ,
, ![]() )和(
)和(![]() ,
,![]() )、(1,0)和(4,0)、(0,3)和(5,3).
)、(1,0)和(4,0)、(0,3)和(5,3).
【解析】
(1)分别把x=0,y=0代入一次函数表达式得:点C、B的坐标分别为(0,3)、(4,0),同理将点B、C的坐标代入二次函数表达式即可求解;
(2)直线y=-![]() x和直线BC平行,直线y=-
x和直线BC平行,直线y=-![]() x和抛物线的交点就是满足条件的点P,即可求解;
x和抛物线的交点就是满足条件的点P,即可求解;
(3)分O′B′在水平位置时、O′C′在水平位置时、B′C′在水平位置时,三种情况分别求解即可.
解:(1)分别把x=0,y=0代入一次函数表达式得:
点C、B的坐标分别为(0,3)、(4,0),
将点B、C的坐标代入二次函数表达式得:
![]() ,
,
解得:![]() ,
,
故抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x+3;
x+3;
(2)直线y=﹣![]() x和直线BC平行,
x和直线BC平行,
直线y=﹣![]() x和抛物线的交点就是满足条件的点P,
x和抛物线的交点就是满足条件的点P,
则 ,
,
解得:![]() ,
,
即当(2,﹣![]() )时,两个三角形面积相同;
)时,两个三角形面积相同;
(3)抛物线的对称轴为:x=![]() ,
,
①当O′B′在水平位置时,如图2所示,
O′B′=4,则点B′和O′的横坐标分别为![]() 、
、![]() ,
,
将横坐标代入二次函数表达式得:y=![]() ,
,
故此时的“卡点对”坐标为(![]() ,
,![]() )和(
)和(![]() ,
,![]() );
);
②当O′C′在水平位置时,
O′C′=3,则点B′和O′的横坐标分别为4、1,
将横坐标代入二次函数表达式得:y=0,
故此时的“卡点对”坐标为(1,0)和(4,0);
③当B′C′在水平位置时,
同理可得:此时的“卡点对”坐标为(0,3)和(5,3);
故抛物线上所有“卡点对”的坐标(![]() ,
,![]() )和(
)和(![]() ,
,![]() )、(1,0)和(4,0)、(0,3)和(5,3).
)、(1,0)和(4,0)、(0,3)和(5,3).

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案