题目内容
【题目】如图AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C作DC⊥OA,交AB于点D.
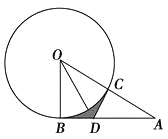
(1)求证:∠CDO=∠BDO;
(2)若∠A=30°,⊙O的半径为4,求阴影部分的面积(结果保留π).
【答案】(1)见解析 (2)![]() -
-![]()
【解析】
(1)证明:AB切⊙O于点B,
∴OB⊥AB,即∠B=90°.
又∴DC⊥OA,∴∠OCD=90°.
在Rt△COD与Rt△BOD中,OD=OD,OB=OC,
∴Rt△COD≌Rt△BOD.
∴∠CDO=∠BDO.
(2)在Rt△ABO中,∠A=30°,OB=4,
∴∠BOC=60°,
∵Rt△COD≌Rt△BOD,
∴∠BOD=30°,
∴BD=OB·tan 30°=![]() .
.
∴S四边形OCDB=2S△OBD=2×![]() ×4×
×4×![]() =
=![]() .
.
∵∠BOC=60°,
∴S扇形OBC=![]() =
=![]() .
.
∴S阴影=S四边形OCDB-S扇形OBC=![]() -
-![]() .
.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
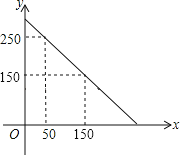
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.