题目内容
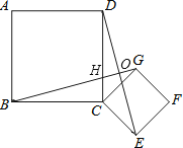
【题目】如图,四边形ABCD与四边形DEFG都是正方形,设AB =a, DG = b(a> b).
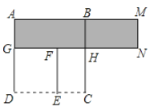
(1)写出AG的长度(用含字母a、b的式子表示);
(2)观察图形,请你用两种不同的方法表示图形中阴影部分的面积,此时,你能获得一个因式分解公式,请将这个公式写出来;
(3)如果正方形ABCD的边长比正方形DEFG的边长多2cm,它们的面积相差20cm2,试利用(2)中的公式,求a、b的值.
【答案】(1)a-b;(2)![]() ;(3)a=6,b=4
;(3)a=6,b=4
【解析】
(1)根据正方形的性质和![]() 即可求出AG的长度;
即可求出AG的长度;
(2)用两种不同的方法表示图形中阴影部分的面积:①求长为![]() ,宽为
,宽为![]() 的矩形的面积;②通过
的矩形的面积;②通过![]() 可得阴影部分面积=四边形ABCD的面积-四边形DEFG的面积,可得
可得阴影部分面积=四边形ABCD的面积-四边形DEFG的面积,可得![]() ;
;
(3)根据正方形ABCD的边长比正方形DEFG的边长多2cm,它们的面积相差20cm2可得![]() ,代入原式并联立方程即可求出a、b的值.
,代入原式并联立方程即可求出a、b的值.
(1)∵四边形ABCD与四边形DEFG都是正方形,设AB =a, DG = b(a> b)
∴![]()
∴![]()
(2)由题意得
![]()
∵![]()
∴![]()
∴![]()
(3)∵正方形ABCD的边长比正方形DEFG的边长多2cm,它们的面积相差20cm2
∴![]()
将![]() 代入
代入![]() 中
中
![]()
解得![]()
联立得
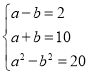
解得![]() .
.

练习册系列答案
相关题目
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
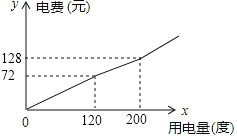
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?