题目内容
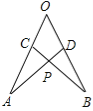
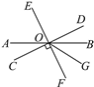
【题目】如图，直线AB，CD，EF交于点O，OG平分∠BOF，且CD⊥EF，∠AOE＝64°，求∠AOF，∠DOG的度数．
【答案】∠DOG＝58°. ∠AOF＝116°
【解析】
根据垂线的定义，可得∠COE=∠COF，根据角的和差，可得∠AOF，根据对顶角的性质，可得∠BOF=∠AOE，∠DOB=∠AOC，根据角的和差，可得答案．
∵∠AOE＋∠AOF＝180°，∠AOE＝64°，
∴∠AOF＝180°－64°＝116°.
∵CD⊥EF，∴∠COE＝∠COF＝90°.
由角的和差，得
∠AOC＝∠AOF－∠COF＝26°.
由对顶角相等，得
∠BOF＝∠AOE＝64°，∠DOB＝∠AOC＝26°.
由OG平分∠BOF，
得∠BOG＝
∠BOF＝32°，
由角的和差，得∠DOG＝∠DOB＋∠BOG＝26°＋32°＝58°.
练习册系列答案
相关题目
【题目】我市某工艺厂为配合北京奥运，设计了一款成本为20元∕件的工艺品投放市场进行试销．经过调查，得到如下数据：
销售单价x（元/件） | … | 30 | 40 | 50 | 60 | … |
每天销售量y（件） | … | 500 | 400 | 300 | 200 | … |
（1）把上表中x、y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；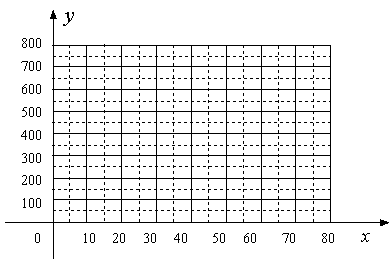 
（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？（利润=销售总价﹣成本总价）
（3）当地物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？
