题目内容
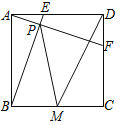
【题目】如图，正方形ABCD中，AB=2，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP的最小值为 ．
【答案】
【解析】
解：如图作点D关于BC的对称点D′，连接PD′，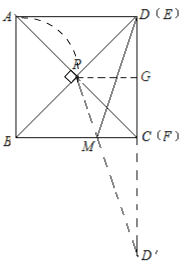
由轴对称的性质可知：MD=D′M，CD=CD′=2
∴PM+DM=PM+MD′=PD′
过点P作PG垂直DC，垂足为G，
易证AF⊥BE，故可知P的轨迹为以AB为直径的四分之一圆弧上，当点E与点D重合，点F与点C重合时，PG和GD′均最短，
∴此时，PD′最短．
∵四边形ABCD为正方形，
，
∴GD′=3．
在Rt△PGD′中，由勾股定理得：
．
故答案为：．
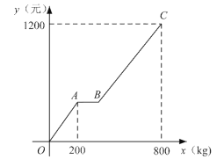
【题目】某商店代理销售一种水果，六月份的销售利润
（元）与销售量
之间函数关系的图像如图中折线所示．请你根据图像及这种水果的相关销售记录提供的信息，解答下列问题：
日期 | 销售记录 |
6月1日 | 库存 |
6月9日 | 从6月1日至今，一共售出 |
6月10、11日 | 这两天以成本价促销，之后售价恢复到10元/ |
6月12日 | 补充进货 |
6月30日 |
|
（1）截止到6月9日，该商店销售这种水果一共获利多少元？
（2）求图像中线段
所在直线对应的函数表达式．
【题目】4月23日是世界读书日，校文学社为了解学生课外阅读的情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：
收集数据：从学校随机抽取20名，进行了每周用于课外阅读时间的调查，数据如下（单位：
）：
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据：按如下分数段整理样本数据并补全表格：
|
|
|
| |
等级 |
|
|
|
|
人数 | 3 |
| 8 | 4 |
分析数据：补全下列表格中的统计量：
平均数 | 中位数 | 众数 |
80 |
|
|
得出结论：
（1）请写出表中
_________；
_________
；
__________；
（2）如果该校现有学生7500人，估计等级为“
”的学生有_________名；
（3）假设平均阅读一本课外书的时间为
，请你选择一种统计量估计该校学生每人一年（按52周计算）平均阅读多少本课外书？