��Ŀ����
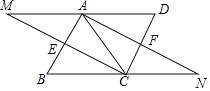
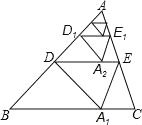
����Ŀ����ͼ������ABC���Ź�AP�е�D��ֱ���۵���ʹ��A����B C���ϵ�A1������Ϊ��1�β������ۺ�DE��BC�ľ����Ϊh1����ԭֽƬ���ٽ���ADE���Ź�AD�е�D1��ֱ���۵���ʹ��A����DE���ϵ�A2������Ϊ��2�β������ۺ�D1E1��BC�ľ����Ϊh2���������������ϲ�����ȥ��������2018�β�����õ����ۺ�D2017E2017��BC�ľ����Ϊh2018����h1=1����h2018��ֵΪ��������
A. 2��![]() B.
B. ![]() C. 1��
C. 1��![]() D. 2��
D. 2��![]()
���𰸡�A
��������
�����е�����ʼ��۵������ʿɵ�DA=DA'=DB���Ӷ��ɵá�ADA'=2��B������۵������ʿɵá�ADA'=2��ADE���ɵá�ADE=��B���̶��ж�DE��BC���ó�DE�ǡ�ABC����λ�ߣ�֤��AA1��BC���õ�AA1=2�����h1=2-1=1��ͬ��h2=2-![]() ��h3=2-
��h3=2-![]()
![]() =2-
=2-![]() �����Ǿ�����n�β�����õ����ۺ�Dn-1En-1��BC�ľ���hn=2-
�����Ǿ�����n�β�����õ����ۺ�Dn-1En-1��BC�ľ���hn=2-![]() ���ݴ˿ɵô𰸣�
���ݴ˿ɵô𰸣�
�⣺����AA1��
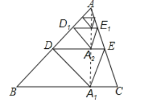
���۵������ʿɵã�AA1��DE��DA=DA1��
�֡�D��AB�е㣬
��DA=DB��
��DB=DA1��
���BA1D=��B��
���ADA1=2��B��
�֡ߡ�ADA1=2��ADE��
���ADE=��B��
��DE��BC��
��AA1��BC��
��AA1=2��
��h1=2-1=1��
ͬ����h2=2-![]() ��h3=2-
��h3=2-![]()
![]() =2-
=2-![]() ��
��
��
�ྭ����n�β�����õ����ۺ�Dn-1En-1��BC�ľ���hn=2-![]() ��
��
��h2018=2-![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ӿȪ�����й����۽�֮�磬��֪ij�۽���ֲ���ү���۽۳ɱ�Ϊ2Ԫ/ǧ�ˣ������δ��90���۽۵����۵���p��Ԫ/ǧ�ˣ���ʱ��t���죩֮��ĺ�����ϵʽΪp=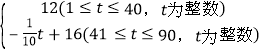 �����۽۵�������y��ǧ�ˣ���ʱ��t���죩����һ�κ�����ϵ���䲿���������±���ʾ��
�����۽۵�������y��ǧ�ˣ���ʱ��t���죩����һ�κ�����ϵ���䲿���������±���ʾ��
ʱ��t/�� | 1 | 10 | 20 | 40 | 70 | 90 |
��������y/ǧ�� | 105 | 150 | 200 | 300 | 450 | 550 |
��1����y��t֮��ĺ�������ʽ��
��2����δ��90��������У�Ԥ����һ�����������������������������Ϊ����Ԫ��
��3����ʵ�����۵ĺ�50���У����ү����ÿ����1ǧ���۽۾;���nԪ����n��5�������ض�ͯ��Ϊ��ѧ�����۹����з��ү���֣�ǡ�ôӵ�51�쿪ʼ����ǰһ����ȣ��۳���������������������ռ��٣������n��ȡֵ��Χ��